"Cost-Sensitive Self-Training for Optimizing Non-Decomposable Metrics" presented on NeurIPS 2022

Recently, in our joint research with the Indian Institute of Science, we have developed an AI technology called cost-sensitive self-training that can optimize practical real-world metrics which are complex and present it at NeurIPS 2022. In this blog post, we introduce our joint research.

Paper

Title: Cost-Sensitive Self-Training for Optimizing Non-Decomposable Metrics (Harsh Rangwani, Shrinivas Ramasubramanian, Sho Takemori, Kato Takashi, Yuhei Umeda, Venkatesh Babu Radhakrishnan)
Conference: Thirty-sixth Conference on Neural Information Processing Systems (NeurIPS 2022)
link to the accepted paper

Authors of this blog post: Sho Takemori, Harsh Rangwani

Overview

The existing works showed that deep learning models can achieve high classification accuracy if the dataset is sufficiently large. However, in many real-world, we need to optimize for complex metrics like F1 Score, AUC, min-recall (used in Federated Learning), etc. which can only be computed over a set of samples and are not just a simple average of a metric on a single sample known as non-decomposable metrics. For optimization of more complex metrics (such as constrained objectives) rather than classification accuracy with a small labeled dataset, we find conventional methods cannot utilize additional unlabeled data to improve performance.

In this work, we focus on classification metrics, and the following are examples of complex (non-decomposable) metrics for classification.

Maximizing the minimum value of class-wise recalls (worst-case recall, used in Federated Learning [Mohri et al. 2019])
Constrained objectives (e.g. maximizing accuracy subject to the coverage for minority classes is greater than 95%, used in Fairness[Goh et al. 2016] )

Further, the $F_\beta$ score is also an example of a complex non-decomposable metric, and we can optimize it with our method by reducing it to cost-sensitive learning [Eban et al. 2017].

These metrics are particularly useful when we train machine learning models on real-world datasets which are usually long-tailed (class imbalanced). As usually labeling is expensive we assume access to a large long-tailed dataset, with only a fraction of it being labeled. The below picture describes the issues faced when a network is trained on such datasets.

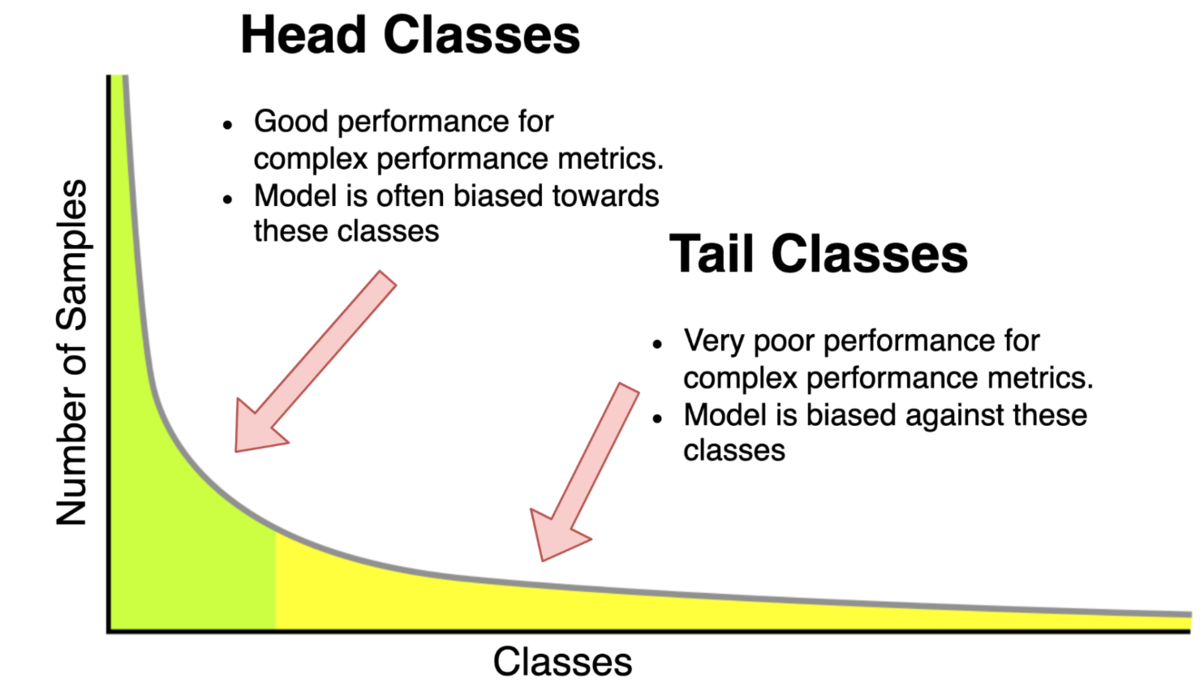
Related Work: We review pros and cons of existing works on optimization of complex metrics and self-training based semi-supervised learning. [Narasimhan et al., 2021] reduced optimization of non-decomposable metrics to cost-sensitive learning (CSL) and proposed (supervised) loss functions. However, their method cannot utilize unlabeled samples. On the other hand, self-training based methods such as FixMatch [Sohn et al. 2020] or UDA[Xei et al. 2020] can achieve high value of accuracy by utilizing unlabeled samples even if labeled dataset is small, however, they cannot optimize complex metrics (Fig 2.).

In this work, we propose Cost-Sensitive Self-Training (CSST) that has the advantage of both CSL and self-training based methods. As it can optimize the non-decomposable (complex metrics) by utilizing unlabeled data effectively. More precisely, we define cost (or equivalently gain) for each entry of a confusion matrix and consider cost-sensitive (or weighted) loss function for self-training based methods. In the learning procedure, the costs dynamically change and therefore the corresponding loss function also changes dynamically to adapt a given metric. For utilizing unlabeled data, we introduce a cost-sensitive (or weighted) consistency regularizer and demonstrate that it provably optimizes the desired non-decomposable metric. We show the practical applicability of proposed CSST by combining it with popular self-training based methods of FixMatch (Image) and UDA (NLP). We find that CSST significantly outperforms baselines on the desired complex metric(s) to be optimized, by effectively utilizing unlabeled data (Fig. 3 shows results on optimization of the worst-case recall on the CIFAR10-LT dataset).

Fig 3. Results on the worst-case recall in CIFAR10-LT

Optimization of non-decomposable metrics and its reduction to cost-sensitive learning

Following [Narasimhan et al., 2021], we now explain how optimization of non-decomposable metrics such as the worst-case recall can be reduced to Cost-Sensitive Learning (CSL). Let $K$ be the number of classes and $F$ a classifier. For a classifier, we denote by $C$ the confusion matrix and $\pi$ the $K$ -dimensional vector representing the class prior of the distribution.

The worst-case recall is defined as the minimum value of recall across all classes, and by definition, it can be written using entries of the confusion matrix (second equality in the following equation). By introducing a vector λ, this can be further formulated as the following objective.

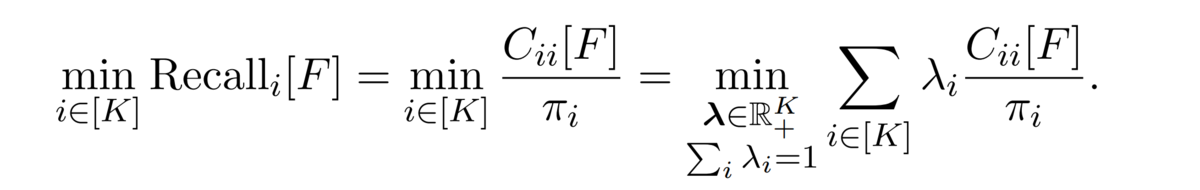
Worst case recall and cost-sensitive learning

Since we want to maximize the min-recall value above with respect to the classifier $F$ , this is a saddle point problem. In practice, we solve this problem by alternatingly updating $F$ and λ. For fixed λ, we maximize the summation of linear weighted terms of the confusion matrix on the rightmost side of the above equation w.r.t. $F$ . We can generalize the above objective further and consider maximization of a linear objective of entries of the confusion matrix w.r.t. F using a matrix $G$ called a gain matrix. The $ij$ entry of the gain matrix represents the reward associated with predicting class $j$ when the true class is $i$ (hence cost-sensitive classification). Similar to the worst-case recall, we can also reduce the optimization of a wide class of non-decomposable metrics to such optimization using the appropriate $G$ matrix.

Objective of cost-sensitive learning (CSL)

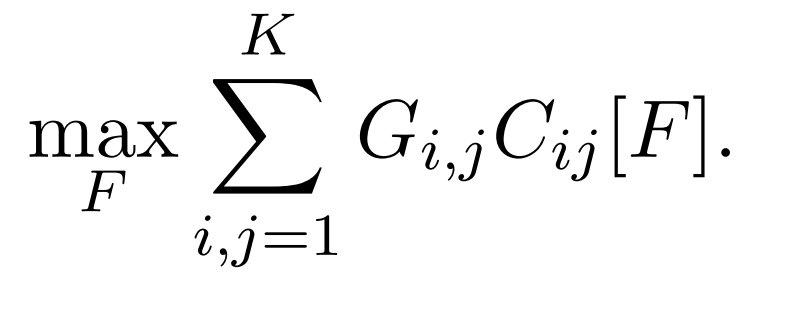
To optimize the CSL objective for deep neural network based classifiers, [Narasimhan et al., 2021] proposed a logit-adjusted(LA) cross-entropy loss function and hybrid loss function and proved their optimality.

Theoretical Loss Function and its Validity

In the previous section, we considered the optimization of non-decomposable metrics in the supervised learning setting. Here, we consider their optimization in the Semi-Supervised Learning (SSL) setting.

We assume access to pseudo labeler $F_{pl}$ that generates pseudo labels, and we want to train a classifier using the pseudo labeler and an unlabeled dataset for optimizing the non-decomposable metric defined through $G$ using CSL.For theoretical analysis, we opt for an equivalent weight matrix w-based formulation of CSL instead of a gain matrix $G$ . For a classifier, we define the weighted error as follows:

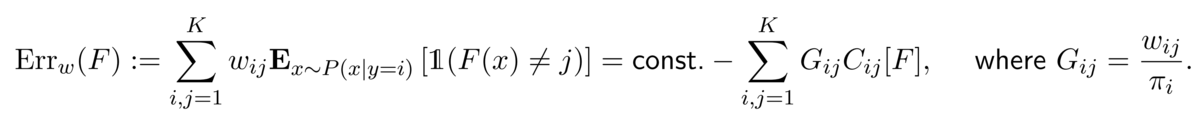
Hence, we observe minimizing the weighted error is equivalent to maximizing the objective of CSL which uses gain matrix $G$ . For a given weight matrix, we propose the following loss function:

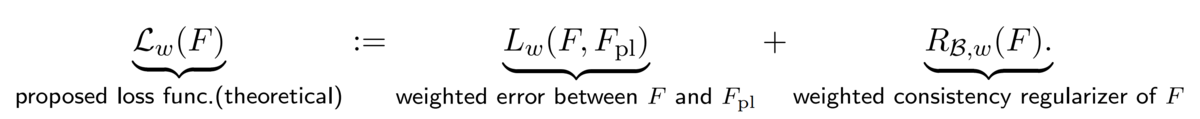
Here the first term of the right-hand side represents the weighted error between a classifier and the pseudo labeler defined below. The second term represents a weighted consistency regularizer. In general, consistency regularizer takes a small value if the classifier is robust to data augmentation. Furthermore, the weighted consistency regularizer is defined so that if the i-th row of the weight matrix $w$ is large then it requires more robustness to augmentations for samples drawn from $P(x | y = i)$ . Although the definition involves distributions $P(x | y = i)$ , in practice, by focusing on unlabeled samples whose pseudo labels are of high confidence, our proposed method will enable the minimization of the proposed loss function.

The following theorem shows that the proposed loss minimization leads to the optimization of the desired metric. For simplicity, we omit technical details regarding assumptions and only provide an informal statement.

Theorem (Informal) Suppose that the pseudo labeler has reasonable performance w.r.t. the weighted error $Err_w$ , a weighted distribution defined by distributions $P(x | y = i)$ satisfies a natural property called the expansion property. Further, there exists an optimal classifier for which $Err_w$ is small and it is sufficiently robust to data augmentation. The learned classifier by the proposed loss function i.e.:

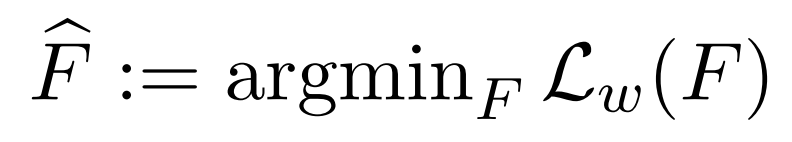
satisfies the following inequality:

Ignoring the second term on the right-hand side, this inequality shows that the learned classifier (i.e. $\widehat{F}$ ) has superior performance than the pseudo labeler in terms of the weighted error (i.e., in terms of CSL). This theorem shows that by introducing an appropriately defined weighted consistency regularizer, one can achieve an improved classifier on desired non-decomposable metric than the pseudo labeler in the semi-supervised setting.

This theorem generalizes a theorem proved by [Wei et al. 2021], where they proved a similar result for accuracy. Although they considered the case when supports of distributions $P(x | y = i)$ are disjoint, we consider a more generalized setting since their assumption implies a vacuous result in our problem setting.

Cost-Sensitive Self-Training in practice

In the previous section, we proposed a theoretical loss function and proved its effectiveness for self-training. Here, we propose a practical loss function that can be used for optimizing deep neural nets for optimizing non-decomposable metrics. Similar to existing self-training based methods (such as FixMatch(Sohn et al. 2020)), we define our loss as a sum of supervised and unsupervised loss functions. Here, as a supervised loss function, we use loss functions for CSL proposed by [Narasimhan et al, 2021].

Proposed loss function for CSST in practice

The unsupervised loss function (i.e weighted consistency regularization) is defined as follows:

Eq1. Proposed unsupervised loss function for CSST in practice

Here, $\ell_u^{wt}$ is a weighted loss function using pseudo labels defined as follows:

Eq2. weighted loss function using pseudo labels

The other notations are provided below.

If we focus on pseudo labels with high confidence, then the unsupervised loss function can be related to the weighted consistency regularizer defined in the previous section (c.f. Appendix B in the paper). In addition, the indicator function in Eq. 1 is required to filter out samples with pseudo labels of low confidence. Self-training algorithms like FixMatch also filter out such samples using a simple threshold mechanism on confidence, but in our case, we need a thresholding mechanism that takes into account the given gain matrix for optimizing our desired metric. The following figure illustrates our novel CSST approach for FixMatch (fig credits: [Sohn et al. 2020]).

Experimental Results

Using a long-tailed image dataset called CIFAR10-LT (displayed in Fig. 5), we empirically compare our method to the baselines (we also obtain similar results on multiple datasets including NLP datasets, for which we have provided details in our paper).

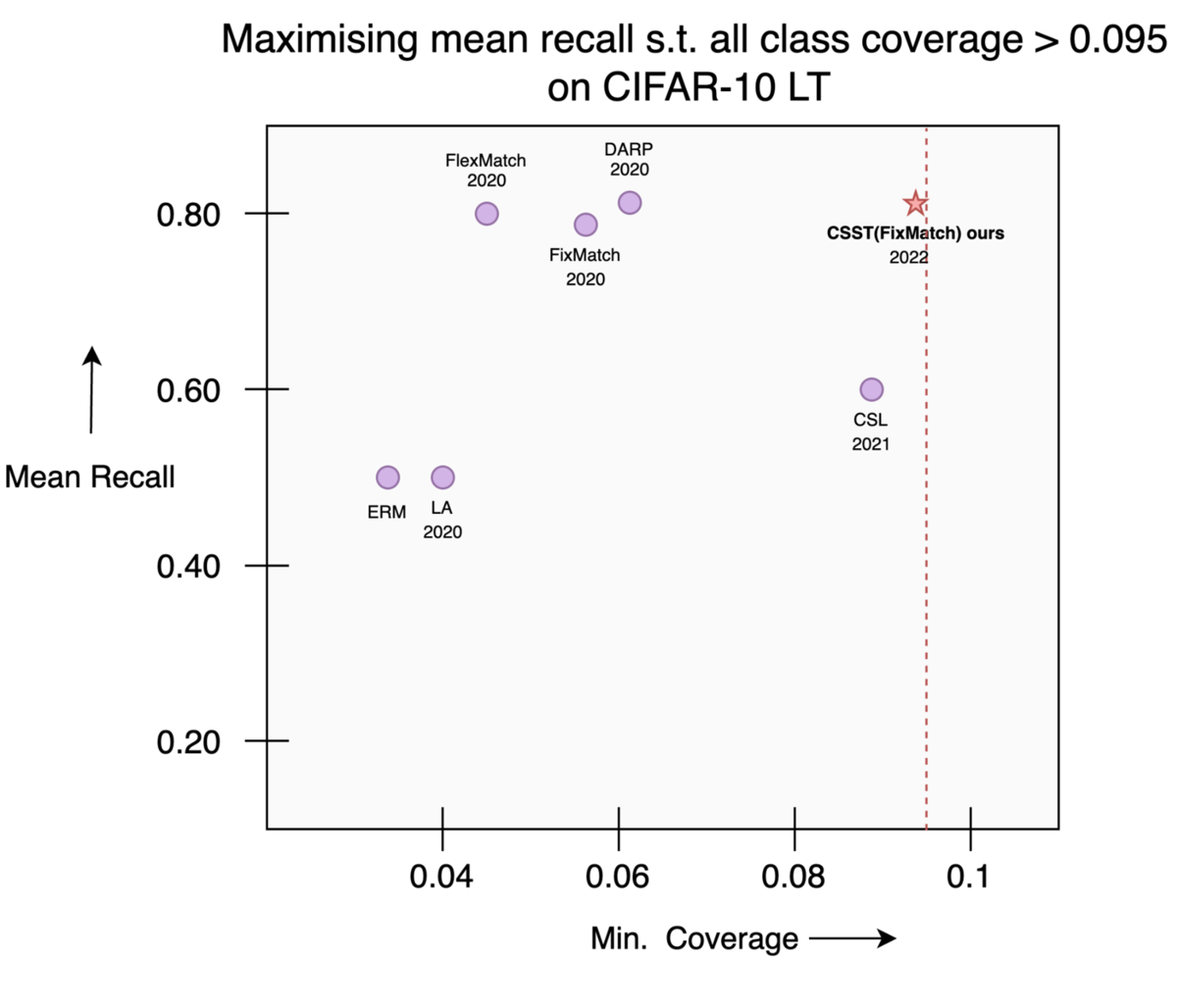
In the experiments, we consider the optimization of two non-decomposable objectives, the worst-case recall and a constrained objective called where the objective is to maximize the mean recall such that the probability of predicting a particular of each class (i.e. coverage) is greater than 0.095 (1/K). Fig. 6 below shows the results for the worst-case recall. From the figure, we see that supervised methods such as ERM, CSL, LA [Menon et al. 2020] cannot utilize unlabeled data, therefore they have inferior performance than the proposed method CSST. Further, we see that the proposed method outperforms existing self-training based methods such as FixMatch and FlexMatch in terms of the worst-case recall. Further, the proposed method outperforms DARP which is a state-of-the-art self-training based method for long-tailed datasets in terms of worst-case recall. In addition, Fig. 7 shows that the existing self-training based methods cannot handle constrained objectives properly. Whereas with CSST we achieve superior mean recall while satisfying coverage constraints.

Fig. 6 Experimental Results on the worst-case recall

Fig. 7 Experimental Results on the coverage objective

Conclusion and Closing Remarks

In this work, we introduced Cost-Sensitive Self-Training (CSST) for optimizing practical real-world metrics which are often non-decomposable. CSST allows the optimization of such metrics by effectively utilizing unlabeled data, through weighted consistency regularization. The proposed regularization mechanism can be easily plugged into practical self-training methods like FixMatch, UDA etc.. We find that CSST leads to significant improvements in the performance of desired non-decomposable metrics while maintaining decent performance on generic metrics like accuracy. Extending CSST for practical fairness applications is a good direction for future work.

Fujitsu Research seeks for new employees and interns. If you are interested in these opportunities, please contact Hiro Kobashi, Project Director in Autonomous Learning Project for a casual meeting (Sorry that the webpage is written in Japanese, but he accepts the chat in English).

References

Harikrishna Narasimhan and Aditya K Menon. Training over-parameterized models with non-decomposable objectives. Advances in Neural Information Processing Systems, 34, 2021
Qizhe Xie, Zihang Dai, Eduard Hovy, Thang Luong, and Quoc Le. Unsupervised data aug- mentation for consistency training. Advances in Neural Information Processing Systems, 33: 6256–6268, 2020
Jaehyung Kim, Youngbum Hur, Sejun Park, Eunho Yang, Sung Ju Hwang, and Jinwoo Shin. Distribution aligning refinery of pseudo-label for imbalanced semi-supervised learning, Advances in Neural Information Processing Systems, 34, 2021
Aditya Krishna Menon, Sadeep Jayasumana, Ankit Singh Rawat, Himanshu Jain, Andreas Veit, and Sanjiv Kumar. Long-tail learning via logit adjustment. In International Conference on Learning Representations, 2020
Colin Wei, Kendrick Shen, Yining Chen, and Tengyu Ma. Theoretical analysis of self-training with deep networks on unlabeled data. In International Conference on Learning Representation, 2021
Elad Eban, et al. Scalable learning of non-decomposable objectives, Artificial intelligence and statistics. PMLR, 2017
Kihyuk Sohn, David Berthelot, Nicholas Carlini, Zizhao Zhang, Han Zhang, Colin A Raffel, Ekin Dogus Cubuk, Alexey Kurakin, and Chun-Liang Li. Fixmatch: Simplifying semi-supervised learning with consistency and confidence. Advances in Neural Information Processing Systems, 33 2020
Mohri, Mehryar, Gary Sivek, and Ananda Theertha Suresh. "Agnostic federated learning." International Conference on Machine Learning. PMLR, 2019.
Goh, Gabriel, et al. "Satisfying real-world goals with dataset constraints." Advances in Neural Information Processing Systems 29 (2016).