
はじめに
こんにちは、人工知能研究所の苗村と竹森です。2025年2月25日~3月4日に開催された人工知能に関する国際会議 AAAI 2025 にて、複雑で高コストな最適化問題を効率よく解くためのベイズ最適化手法について発表したので、その内容を紹介します。
採択論文
- タイトル:Regional Expected Improvement for Efficient Trust Region Selection in High-Dimensional Bayesian Optimization
- 著者:Nobuo Namura, Sho Takemori
- 発表会議: The 39th AAAI Conference on Artificial Intelligence (AAAI 2025)
- 論文へのリンク(arXiv)
研究背景と対象
高コストなブラックボックス最適化問題
自動車や家電のような工業製品の設計や、創薬、材料開発、機械学習モデルのハイパーパラメータ調整といった現実で直面する最適化問題では、最適化したい性能指標(目的関数と呼びます)の具体的な数値を得るのに、非常に長い時間がかかったり、多額の費用が発生することがあります。自動車であれば、目的関数である燃費を評価するのに高価な試作品を使った実験やコンピュータを使った長時間のシミュレーションが必要です。 さらに、このような高コストな最適化問題の中には、設計案に対する目的関数の数値のみが計測でき、その他の情報(設計パラメータに対する感度など)が得られないというブラックボックス性を持っているものが数多くあります。したがって、設計パラメータ(設計変数と呼びます)を微小変化させた場合の目的関数の変化を知るためには、高コストの実験やシミュレーションを設計変数の数と同じ回数実行する必要があり、それだけで途方もないコストが発生してしまいます。
ベイズ最適化
高コストなブラックボックス最適化問題に対しては、ベイズ最適化という方法が頻繁に用いられます。最も一般的なガウス過程モデルを用いたベイズ最適化は以下のような手順で実行されます。
- ランダムに選択したいくつかの設計案に対して目的関数を評価したデータセット(サンプル点)を用意する
- 既存のサンプル点を用いてガウス過程という方法で、任意の設計案に対する目的関数の値を予測するモデル(ガウス過程モデル)を訓練する
- ガウス過程モデルを使って目的関数が改善しそうな設計案や、モデルによる目的関数の予測誤差が大きい設計案を特定し、その設計案の目的関数を評価してサンプル点に追加する
- 満足いく解が得られるか、予算の上限まで2, 3を繰り返す
ガウス過程モデルを用いると、図1のように任意の設計案に対する目的関数の予測値だけでなく、予測の誤差範囲を同時に算出することができます。ベイズ最適化では、単に予測される目的関数の値が良さそうなところにサンプル点を追加する(Exploitation、活用と呼びます)だけでなく、モデルの予測誤差が大きいところ(目的関数がいくつになるかよくわからないところ)へのサンプル点の追加(Exploration、探索と呼びます)をバランスよく行い、効率的に最適解を得ることをめざします。
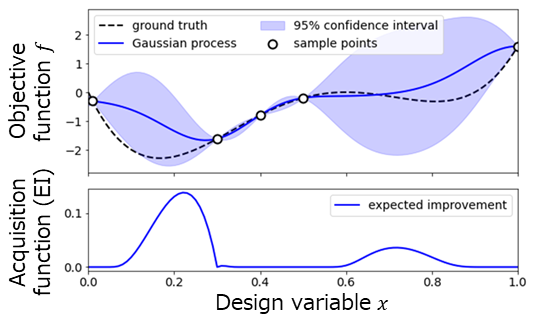
活用と探索のバランスを考慮して、次に追加すべきサンプル点としての相応しさを表す指標を獲得関数と呼び、代表的なものとして期待改善量(Expected Improvement: EI)というものがあります。EIは、これまでに得たサンプル点の中の最も優れた目的関数の値に対して、追加しようとするサンプル点によって、どれくらいの改善が見込めるかの期待値を計算したものです。図1のように、EIは目的関数の値が良さそうなところ(最小化問題の場合、青線の値が小さいところ)や、予測誤差の大きなところ(青塗りの上下幅が広いところ)で大きな値を取り、EIが最大となるところにサンプル点に追加することで、効率よく最適化を進めることができます。
高次元問題のベイズ最適化
ところが、通常のベイズ最適化が上手く機能するのは、設計変数が10個程度までの低次元の最適化問題に限定され、設計変数が100個程度ある高次元の問題では全く通用しなくなります。これは、問題の次元が大きくなると、ガウス過程でモデル化すべき設計案の範囲や数(設計空間と呼びます)が指数的に増加し、複雑な問題になるという次元の呪いによるものです。一方、問題の次元が増えても目的関数の評価コストは変化しないか、さらに高コスト化することが多いため、予算から決まるサンプル点の総数(数十~数千)はほとんど変化しません。結果として設計空間内のサンプル点の密度が低下し、ガウス過程モデルによる目的関数の予測精度が著しく悪化してしまいます。
この問題を解決するため、先行研究として信頼領域ベイズ最適化(Trust Region Bayesian Optimization: TuRBO)[1]という方法が提案され、数百次元の問題まで効率的な最適化が可能であることが示されました。この方法では信頼領域と呼ばれる設計空間の一部分に対してのみ、サンプル点の追加を許容することで信頼領域内でのサンプル点の密度を高め、ガウス過程モデルの予測精度を維持しています。信頼領域は、それまでに発見したサンプル点の中で最も優れたものを中心とする超立方体として定義され、その大きさは最適化が進むにつれて小さくなっていきます。そして、信頼領域の大きさが所定の値よりも小さくなると、その信頼領域での最適化を終了し、全てのサンプル点を取り除いた新しい信頼領域で同様の最適化をリスタートします。
TuRBOは非常に優れたベイズ最適化手法ですが、最適化開始時やリスタート時の信頼領域はランダムに生成されたサンプル点の中で最も優れた解を中心に一定の大きさで生成されます。このため、信頼領域に大域的最適解と呼ばれる山の山頂にあたる真の最適解が含まれず、山の頂上に向かう途中の丘の頂のような局所最適解と呼ばれる解しか得られないことが多々あります。また、リスタート時には、それまでに得たサンプル点の情報を一切利用せずに新しい信頼領域を選択するため、同じ場所を複数回探し回るなどして、一向に大域的最適解に近づかないことも考えられます。
研究目的
私たちの研究では、TuRBOや信頼領域を利用する他の最適化手法に対して、大域的最適解を含む可能性の高い信頼領域を効率的に特定する方法を提供し、理論解析と数値実験でその効果を実証しています。
提案手法:領域平均獲得関数 Regional Expected Improvement
「良さそうな信頼領域を見つける」というと、通常のベイズ最適化のように既存の全てのサンプル点を用いてガウス過程モデルを訓練し、EIが最大となる位置を中心とした信頼領域を作る、というアイデアが最初に出てきます。しかし、EIは次の一点を見つけるための指標であるため、このように信頼領域を選択すると、信頼慮域内でEIの高い場所がごく一部しか存在しないということが起こりえます。一度、信頼領域を選択するとその中でTuRBOのような局所探査と呼ばれるアルゴリズムが数十~数百回にわたってサンプル点を追加し続けるため、もしもEIが最大だった位置の近くに大域的最適解が存在しない場合には、無駄な局所探査を繰り返すことになります。
このようなリスクを避けるために、私たちの方法ではEIのような通常の獲得関数の信頼領域内での平均値を計算した領域平均獲得関数というものを導入します。図2では、1次元の最小化問題に対して、EIを領域平均獲得関数に変換したRegional Expected Improvement (REI)がどのような分布になるかを示しています。左図は初期の信頼領域の選択時、右図はリスタート時の様子に対応しています。左図を見ると、EIは左端で最大となるのに対して、REIは右端付近で最大となっており、REIを利用して信頼領域を選択するとEIとは異なる領域が選択されることがわかります。この図の場合、EIは左端で最大値を取りますが分布が狭く、左端から少し離れると急激にEIが低下するのに対し、右端付近ではEIは幅広の分布を持っているため、広範囲で目的関数の改善が可能であることがわかります。このようにREIを用いて、EIが幅広の分布を持つところやEIが多数の山を持つところを信頼領域として選択することで、TuRBOのようなアルゴリズムはリスタートの度に着実に目的関数を改善していくことができます。
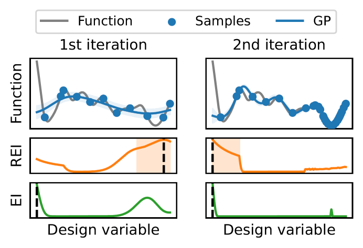
REIとEIによる領域選択の比較
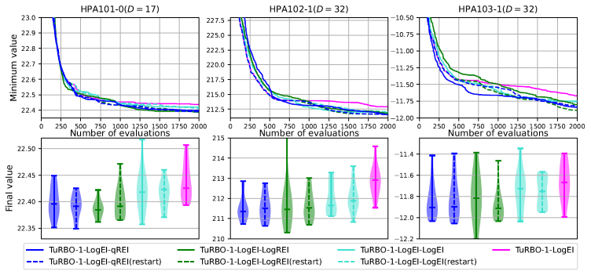
理論解析では、領域平均獲得関数を元の目的関数を領域平均してから獲得関数を計算するという操作に置き換えて考えることで、累積リグレットと呼ばれるアルゴリズムの最適化能力を表す指標(小さい方が良い)の上界が、領域平均獲得関数の導入で通常の獲得関数を用いた場合以下の範囲に抑えられることを証明しました。 また、REIやEIによる領域選択をTuRBOに導入し、人力飛行機の設計に関する三種の最適化ベンチマーク問題(最小化問題)でも対応する比較実験を行いました。図3に示すように、信頼領域の選択にREI(青または緑の4つのプロット)を用いることで、EI(水色の2つのプロット)を用いた場合や、通常のTuRBO(ピンクのプロット)よりも、目的関数を改善できることが実証されました。青と緑のプロットではREIの実装方法が異なっており、各色の実線のプロットはTuRBOの初期とリスタート時の領域選択にREIやEIを用いた結果、破線のプロットはリスタート時のみにREIやEIによる領域選択を適用しています。
なお、検証に用いた人力飛行機設計の最適化ベンチマーク問題[2]も苗村が作成しており、こちらはEMO 2025という最適化分野の国際会議で発表しています。
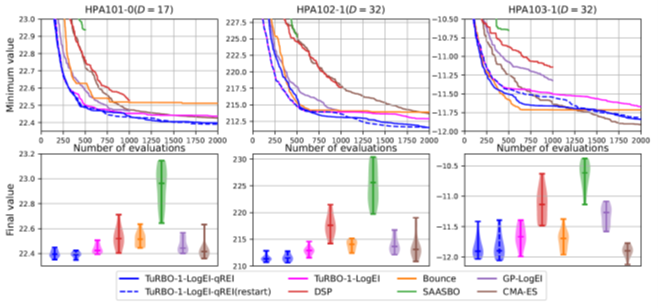
最新のアルゴリズムとの比較
同様の三種のベンチマーク問題で、提案するREIを用いたTuRBO(青の2つのプロット)と、最新の高次元ベイズ最適化手法[3-5]、通常のベイズ最適化、進化計算手法[6]を比較すると、2つの問題で最高性能となり、残りの問題でも予算の上限に依らず安定して優れた性能を発揮しました。これらの問題は17次元、32次元のものであり、サンプル点の数が2000個に至るまでの間に概ね2~4回のリスタートが発生することで、REIによる領域選択の効果が明確に表れています。
論文では100次元程度の問題まで、REIによるTuRBOの性能改善が可能であることを実証していますが、これらの問題ではサンプル点が2000個になってもTuRBOのリスタートが発生せず、REIの効果が初期の信頼領域選択に限定されてしまいました。より高次元の問題においてREIによる領域選択の効果を最大限生かすには、TuRBOの収束を早めてリスタートを促進するような工夫が必要だと考えています。
まとめ
私たちの研究では、高コストで高次元なブラックボックス最適化問題を効率よく解くために、TuRBO等の局所探査を実行すべき適切な信頼領域を発見・選択するための領域平均獲得関数を提案し、理論解析と数値実験でその効果を確認しました。このような問題設定は、現実世界の最適化問題でも数多く見受けられるため、その解法が社会に役立つ研究として広まっていくことを期待したいです。
参考文献
- Eriksson, D. et al., Scalable global optimization via local Bayesian optimization, Advances in Neural Information Processing Systems, 32, 2019.
- Namura, N., Single and multi-objective optimization benchmark problems focusing on human-powered aircraft design, International Conference on Evolutionary Multi-Criterion Optimization, pp. 195-210, 2025.
- Eriksson, D. and Jankowiak, M. High-dimensional Bayesian optimization with sparse axis-aligned subspaces, Uncertainty in Artificial Intelligence, pp. 493–503, 2021.
- Papenmeier, L. et al., Bounce: reliable high-dimensional Bayesian optimization for combinatorial and mixed spaces, Advances in Neural Information Processing Systems, 36, pp. 1764–1793, 2023.
- Hvarfner, C. et al., Vanilla Bayesian optimization performs great in high dimensions, International Conference on Machine Learning, 2024.
- Hansen, N. and Ostermeier, A., Completely derandomized self-adaptation in evolution strategies, Evolutionary Computation, 9(2), pp. 159–195, 2001.