
こんにちは、私たちはFujitsu Research of India Pvt. Ltd(FRIPL)の人工知能研究所のVempalli Saketh、Siddartha Reddy Thummaluru、Harsh Pandey、Mahesh Chandranです。本日は、グラフAIをより透明で、信頼でき、実用的なものにするための最新の研究をご紹介できることを嬉しく思います。
以前のブログ記事「10億ノードグラフを「使い切る」:大規模学習と適応型グラフAI」で詳しく説明したように、グラフ構造は現代のデジタルインフラのバックボーンとして確固たる地位を築いています。数十億のつながりを表現するソーシャルネットワークから、広大なトランザクションフローを監視する金融システムまで、業界は大規模な相互接続データセットの処理において大きな進歩を遂げてきました。しかし、これらのスケーラブルなアーキテクチャを構築するにつれて、重要なトレードオフが浮上します。この規模を扱うために必要な途方もない複雑さが、しばしばモデルの不透明さを深めてしまうのです。
すなわち、予測のための処理能力だけでは十分ではないということです。数十億のエッジ上で推論できるようになりましたが、そのため必要な洗練されたアーキテクチャ(グラフニューラルネットワーク(GNN)など)は、パフォーマンスのために透明性を犠牲にすることがよくあります。私たちの経験では、このトレードオフが導入への大きな障壁となります。私たちはこれを「ブラックボックスのジレンマ」と呼んでいます。完璧に機能するモデルがあるにもかかわらず、そのロジックの妥当性を重要なシナリオで検証する能力が欠けているという問題です。
モデルがトランザクションを不正としてフラグを立てたり、新しい薬剤の相互作用を予測したりする場合、関係者は必ず「なぜ?」と尋ねます。この課題に取り組む中で、私たちはグラフAIへの信頼には2つのアプローチが必要であることに気づきました。
説明可能性は最初の重要な要件です。すでに訓練されたブラックボックスモデルがある場合、説明可能性は意思決定を理解可能にすることを目的としています。それは、これらのモデルが学習したパターンを明らかにすることに焦点を当て、信頼と明確さを築き、さらには望ましくないパターンや偏ったパターンを特定して修正することを可能にします。
解釈可能性は2番目の要件です。意思決定が下された後に説明するのではなく、解釈可能性は、モデルが設計上透明であり得るかを問いかけます。計算を行う際に「どう動くかわかる」アーキテクチャを構築し、推論プロセスをモデル自体に内在させることができるでしょうか?
このブログでは、これら2つの概念に関する私たちの画期的な技術を、競合する解決策としてではなく、信頼できるグラフAIの補完的な柱として紹介します。これらは、FRIPLの研究者によって、先日閉幕したサンディエゴ(米国)で開催されたAI研究者の年次総会であるNeurIPS 2025会議で発表されました。
1. グラフの説明可能性:GNNの自然言語による説明
グラフニューラルネットワーク(GNN)は、依然として大部分がブラックボックスモデルです。これまでの研究では、GNNの推論を局所的に(または個々のデータレベルの説明として)、例えばRCExplainer [1]やMEG [2]のように説明するか、大域的な説明はGNNinterpreter [3]やGLGExplainer [4]のようなモチーフ(分類にとって重要なグラフのパターン)発見に大きく依存していました。モデル推論に対する局所的説明は、個々のノードが特定の分類に属する理由を正当化しようとしますが、より根本的な問いには答えられません。
Q: このモデルは、この分類を全体としてどういう考え方で予測しているのか?
私たちは、IITデリーのSayan Ranu教授とその研究グループとの最近の共同研究で、ノード分類におけるこのギャップに取り組み、NeurIPS 2025で口頭発表された「GnnXemplar: Exemplars to Explanations — Natural Language Rules for Global GNN Interpretability」(https://arxiv.org/abs/2509.18376)を発表しました。この論文は、Burouj Armgaan、Eshan Jain、Harsh Pandey、Mahesh Chandran、Sayan Ranuが共著者です。この研究では、複雑な部分グラフパターンに頼るのではなく、大規模言語モデル(LLM)の表現力を活用することで、人々の自然な推論方法とモデルの説明を一致させる人間中心のアプローチを提案しています。
私たちの研究では、GNN予測の効果的な説明は、次の2つの主要な基準を満たす必要があることを示唆しています。
- モデルに忠実であること。つまり、モデルの意思決定プロセスを正確に反映している必要があります。
- 解釈可能であること。グラフ構造に基づくデータ表現の複雑さにもかかわらず、人間が予測の背後にある推論を理解できるようにします。
主要なアイデア:典型理論と自然言語による説明
GnnXemplarは、認知科学の典型理論からインスピレーションを得ています。この理論によれば、人間は抽象的な規則に頼るのではなく、記憶に保存された具体的で代表的な例と比較することで新たに与えられたデータを分類します。
私たちは、このアイデアをGNNの説明可能性にもたらし、与えられた分類に対してモデルが内部的にどのように表現しているかを最もよく捉える典型ノードを特定します。これらの典型ノードは、モデルのグローバルな振る舞いを理解するためのアンカーとして機能します。
特に、主にノード分類データセットで観察されるような大規模で高密度なグラフで説明可能性を高めるためには、複雑さと規模の大きさゆえに、部分グラフの可視化では本質的に効果がありません。代わりに、典型ノードとその関連する集団の共通の特性(これをシグネチャと呼びます)をテキストによる説明に蒸留します。これにより、説明がより直接的で理解しやすくなります。
GnnXemplarの仕組み
以下、図1はGnnXemplarの完全なパイプラインを示しています。パイプラインは2つの段階に分かれています。最初の段階では、各クラスのグラフに典型ノードを発見し、2番目の段階(点線枠の中)では、これらの典型ノードのシグネチャを自然言語表現に変換します。この2つの段階を合わせることで、これらのブラックボックスモデルが計算し学習する高次元表現(埋め込みとも呼ばれる)を人間が読める説明に変換します。
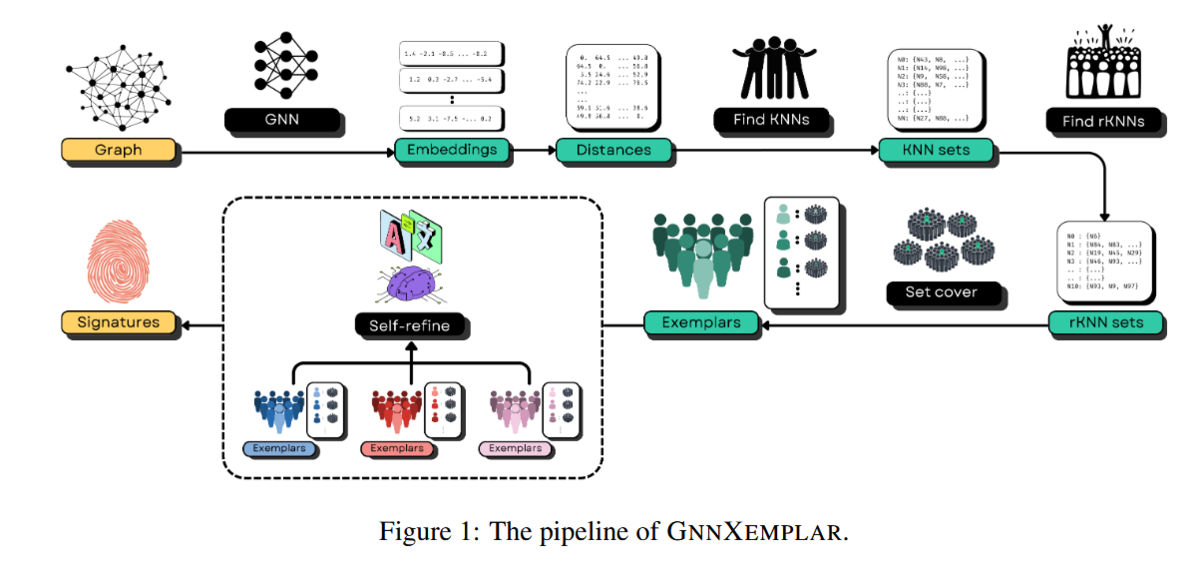
この2つの段階をさらに詳しく見ていきましょう。
1. 典型ノードの発見:
分類を代表する典型ノードを特定することは容易ではありません。私たちはこれを、埋め込み空間におけるカバレッジ最大化問題として定式化します。
- 逆k-近傍(Rev-k-NN): ノードがどの近傍に近いかを尋ねるのではなく、いくつのノードが与えられたノードを最も近い代表と見なすか、つまり、どのノードが最も人気があるかを尋ねます。そのような参照を多く引き付けるノードは、強力な典型ノード候補です。
- 貪欲近似: これらの人気のあるノードからサブセットを選択する際、すべての学習ノードのカバレッジを最適化する必要があります。最適なカバレッジ選択はNP困難(答え合わせは簡単だが答えを見つけるのが非常に大変な問題)であるため、効率的な貪欲戦略を使用して、分類をまとめてよく表す多様な典型ノードのセットを選択します。私たちは、ノードの被覆をどれだけ追加的に拡げられるかを最大化するノードを反復的に選択します。これにより、ほとんどの集団を共有するノード間の冗長性が回避されます。なぜなら、一方を選択すると、他のノードが新たに被覆できる範囲が減少し、選択できる数の制限内でカバレッジと多様性の両方を促進するからです。
2. 典型ノードから自然言語規則へ:
典型ノードが特定されたら、次の課題は自然言語での典型シグネチャの発見です。これを行うために、大規模言語モデル(LLM)の推論能力を活用します。私たちの目標は、GNNの予測に密接に一致する自然言語で表現された記号的規則を導き出すことです。 このアイデアは、LLMにいくつかの正のサンプルといくつかの負のサンプルを与え、正のサンプルには存在するが負のサンプルには存在しないシグネチャを抽出するというものです。このステップを2つの部分に分けます。
- 初期プロンプトの生成:
特定の典型ノードについて、まず、典型ノードとその集団からランダムに選択されたサブセットを含む正のセットを作成します。次に、学習データセットの残りのノードからランダムに選択して負のセットを作成します。正と負のセットが準備できたら、ノードとその近傍をシリアライズし、シグネチャの抽出のためにLLMに渡せるようにします。ブラックボックスGNNが
L-ホップの場合、正および負のセットの各ノードのL-ホップ近傍の概要を提供します。概要には以下が含まれます。- ノードの属性。
- 各ホップのすべてのノードに対するGNN予測クラスラベルの正規化された頻度分布。
- 典型と各ホップレベルのすべてのノード間の属性あたりの平均L1距離。
- 自己洗練、LLMベースの規則生成: 自然言語シグネチャを生成するためにLLMに一度だけクエリを実行するのではなく、より堅牢な反復アプローチを採用しています。LLMは繰り返しプロンプトを与えられ、その出力は保持された検証セットで検証されます。最初のプロンプトでは、LLMにシグネチャの存在をテストするためのPythonコードを生成するよう求められ、次にこの関数から自然言語規則を生成するよう求められます。Python関数は、シグネチャを評価し、失敗ノードを特定し、問題のあるノードでLLMに繰り返し再プロンプトを出すのに役立ち、その結果、徐々に洗練された自然言語シグネチャが得られます。
論文の引用関係ネットワークに基づき論文を分類する場合の、シグネチャの例は次のとおりです。「ノード(論文)がニューラルネットワークについて言及し、少なくとも3つのコンピュータサイエンスノードに接続している場合、ニューラルネットワーク研究論文として分類する。」
GnnXemplarが重要な理由
従来のグローバルな説明技術は、繰り返し現れる部分グラフモチーフに依存することが多く、このアプローチは、そのようなモチーフがまれな大規模な実世界グラフでは機能しません。 GnnXemplarは、シグネチャを使用することで、この主要な制限を克服し、さらに以下を提供します。
- スケーラビリティ: サンプリングベースのRev-k-NNにより、OGB-ArXivのような大規模グラフでも説明が可能です。
- 人間の解釈可能性: ユーザーが、特に密な部分グラフの可視化よりも一貫して好む自然言語のルールを生成します。これは、AIモデル推論の説明を非専門家にも理解できるようにするために特に重要です。
- 高い忠実度: 説明は、モデル自体を単純化することなく、モデルの内部的な推論を正確に反映しています。
- GNNへの忠実性: 高い忠実度とGNNのノード埋め込みの使用により、GNNへの忠実性が高まります。
図2は、様々なデータセットにおける異なるグラフ説明可能性手法を比較し、他の手法よりもGnnXemplarを使用する明確な利点を示しています。ここで注意すべきは、「忠実度」という指標は、説明と真値との整合性を比較するものです。つまり、GNNがあるノードをクラスAと予測した場合、説明可能性手法もそのノードをクラスAと予測すべきである(たとえAがそのノードの真値ではないとしても)。これは、説明可能性手法とブラックボックスGNNモデルとの整合性に関心があり、真値ではないためです。 他のほとんどの手法は、ほとんどがモチーフベースの説明に依存しており、ノード分類では識別できる離散的なモチーフがないことが多いため、まともな忠実度さえ提供できないことがわかります。
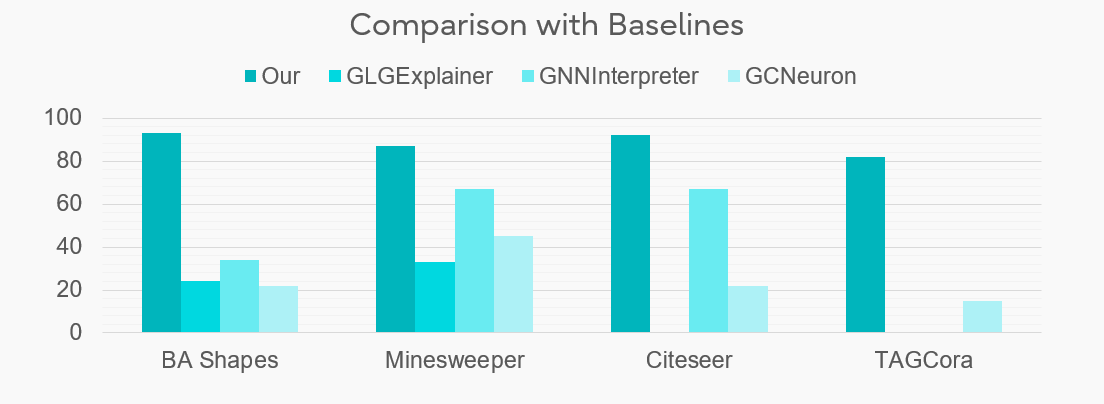
まとめと今後の展望
GnnXemplarは、AIの説明可能性における転換点を示しています。GNNの幾何学的な特徴に対する強みとLLMの言語的推論、そして認知科学の典型理論の心理学的基盤を組み合わせることで、複雑なAIシステムをそれを使用する人間にとって真に透明なものにするためのロードマップを提供します。
現在、このアプローチをさらに実用的で、数百万のノードを持つ巨大な実世界グラフに適用するために修正に取り組んでおりますので、ご期待ください!
2. 自己解釈型グラフモデル:設計による透明性
既存のモデルを説明することは強力ですが、私たちは本質的な透明性に焦点を当てた補完的な方向性も追求しました。それは次の問いです。
本質的な透明性を備えつつ,性能面でも同等である「グラスボックス」アーキテクチャを設計できるだろうか?
これが、自己解釈型グラフモデルの分野へと私たちを導きました。凍結されたモデルの推論を近似する事後アプローチとは異なり、自己解釈型アーキテクチャは推論プロセスを本質的に符号化します。「説明」は別の計算ではなく、モデルが答えに到達するために辿った経路です。
ここでの明確な利点は、忠実性です。説明は計算に内在しているため、モデルが行ったことと説明が述べたことの間にギャップはありません。これにより、提供される推論が予測に直結したものであることが保証されます。さらに、自己解釈型モデルは、しばしばより優れた汎化につながります。モデルに疎で意味のある部分構造(創薬における特定の化学モチーフや不正検出における循環取引ループなど)に焦点を当てることで、ノイズの多い相関関係ではなく、堅牢で因果的なパターンを学習するように促します。これにより、透明であるだけでなく、実世界のデータにおける分布シフトに対してより堅牢なモデルが得られることがよくあります。
私たちは、この分野への最新の貢献、G-NAMRFF (Graph Neural Additive Model with Random Fourier Features) をNeurIPS 2025会議で発表できたことを誇りに思います。
プロジェクトページ、ポスター、論文へのリンク: NeurIPS Poster Interpretable and Parameter Efficient Graph Neural Additive Models with Random Fourier Features
G-NAMRFFの核となるアイデアは、アーキテクチャ図である図3に示されています。
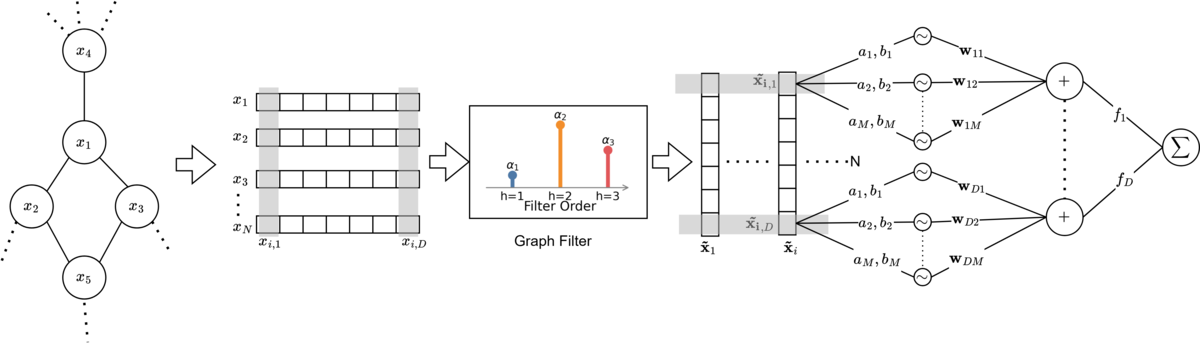
「部分の総和」という哲学
標準的なグラフニューラルネットワークは、高度に絡み合った操作に依存しているため、しばしば不透明です。GNNが隣接ノードからデータを集約する場合、非線形な「ブラックボックス」(通常は多層パーセプトロン)で特徴量を混合し、個々の変数の寄与を追跡することが不可能になります。
G-NAMRFFは、ニューラル加算モデル(NAM)[5]の最近の成功に触発された汎用加算モデル(GAM)アプローチを採用することで、これを解決します。複雑で絡み合った推論過程ではなく、このモデルは個々の特徴の寄与の単純な合計により予測します。
銀行口座が不正利用されているかどうかを予測していると想像してください。標準的なGNNでは、「口座開設からの期間」と「取引金額」が乗算され、変換されるため、どちらがより重要であったかが不明瞭になります。G-NAMRFFでは、モデルは「口座開設からの期間」と「取引金額」に対して別々の特定の形状関数を学習します。最終的なリスクスコアは、これらの独立したスコアの合計にすぎません。
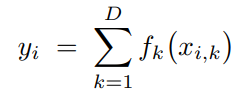
革新的なポイント:ランダムフーリエ特徴を用いたガウス過程
G-NAMRFFの目新しさは、ベイジアンノンパラメトリックモデリングと計算効率の高いディープラーニング近似の原則に基づいた統合にあります。従来、多くのパラメータを必要とする標準的なニューラルネットワーク層を使用して特徴ごとの形状関数f_kを学習する代わりに、G-NAMRFFは各特徴の寄与をガウス過程(GP)を用いて表現します。この設計により、特徴レベルでの解釈可能性を維持しながら、柔軟で不確実性を考慮した関数モデリングが可能になります。
特徴の寄与をGPとして扱うことで、モデルは滑らかで複雑な非線形パターンを学習し、単純な線形関係を強制することなくデータに自然に適合させることができます。これをスケーラブルにするために、ランダムフーリエ特徴(RFF)近似技術[6]を採用しています。
- 暗黙的カーネルマッピング:RFFを使用すると、入力データをランダムな特徴空間にマッピングでき、そこで複雑な非線形カーネル操作が単純な線形内積になります。
- 単層学習:特徴量をこのRFF空間に投影することで、軽量な単層ニューラルネットワークを使用して複雑な形状関数を学習できます。
しかし、効率的な特徴処理は工夫の半分にすぎません。グラフAIの力を真に活用するには、私たちのアーキテクチャは、ノードの特徴を単独で処理するだけでなく、グラフの接続性を本質的に尊重する必要があります。 私たちのアーキテクチャパズルの最後のピースは、「グラスボックス」がグラフを認識したままであることを保証することです。私たちは、ラプラシアン(グラフ構造の特徴を反映した行列)を介してグラフ構造を明示的に組み込んだ特殊なカーネルを開発しました。これにより、モデルが特定の機能の「形状」と影響を学習する際に、ノードを単体で分析するのではなく、ノードの隣接ノードのコンテキストを考慮し、ローカル集約を解釈可能な追加フレームワークに直接統合します。このアーキテクチャは、GNAN [7]のような追加グラフモデルの以前の試みと比較して、改善されたパラメータ効率を達成しています。
変異原性からの例
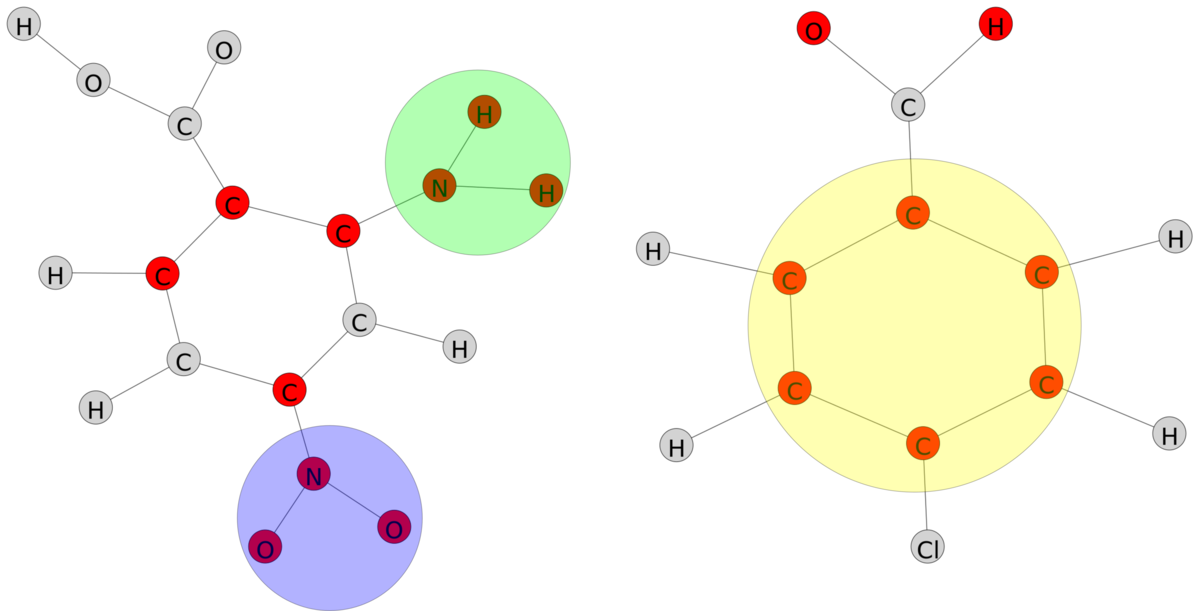
創薬において、分子が変異原性(DNAに突然変異を引き起こす性質)であるかどうかを特定することは極めて重要です。標準的なブラックボックスモデルは、分子が毒性であることを正確に特定するかもしれませんが、化学構造のどの部分が全体的な特性の原因となっているかを示すことができません[8]。G-NAMRFFは、単純な特徴の重要性を超えて、局所的な構造の説明を提供します。グラフの近傍に沿って特徴レベルの属性を集約することで、モデルは予測の原因となっている特定のサブグラフを強調表示します。私たちの実験では、モデルは自動的にニトロ基(NO2)およびアミノ基(NH2)グループと芳香環を抽出し、それらが変異原性の主要なサブ構造であることを強調しました。これは確立された文献と完全に一致しています。これは以下の図に示されています。
結果と考察
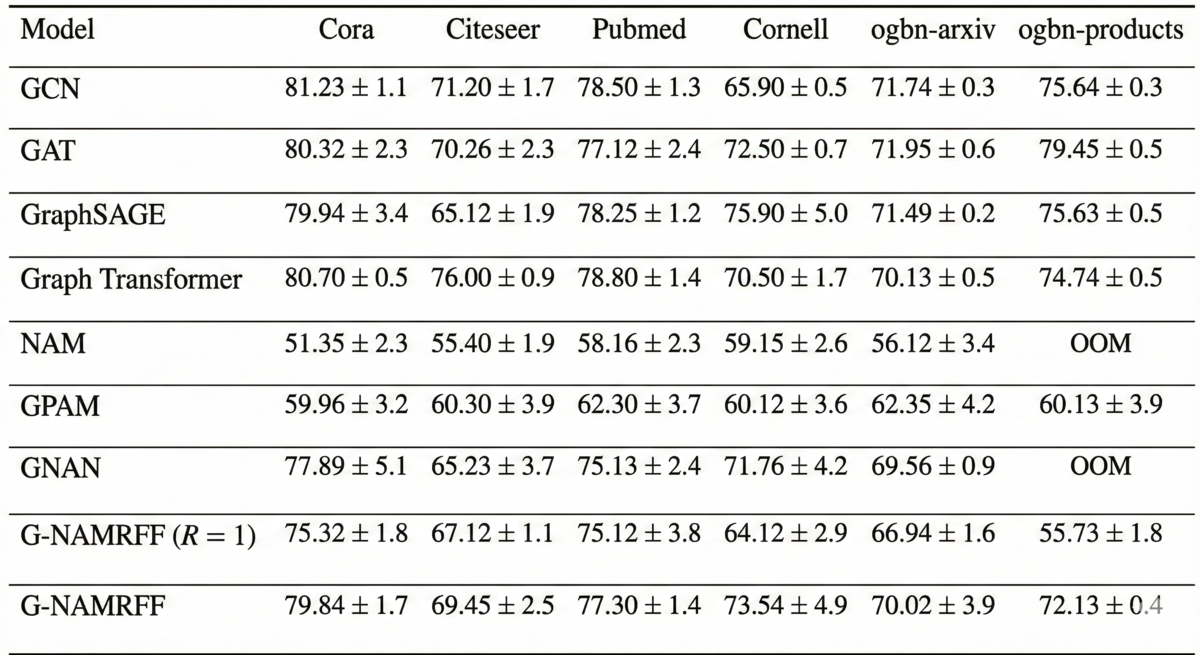
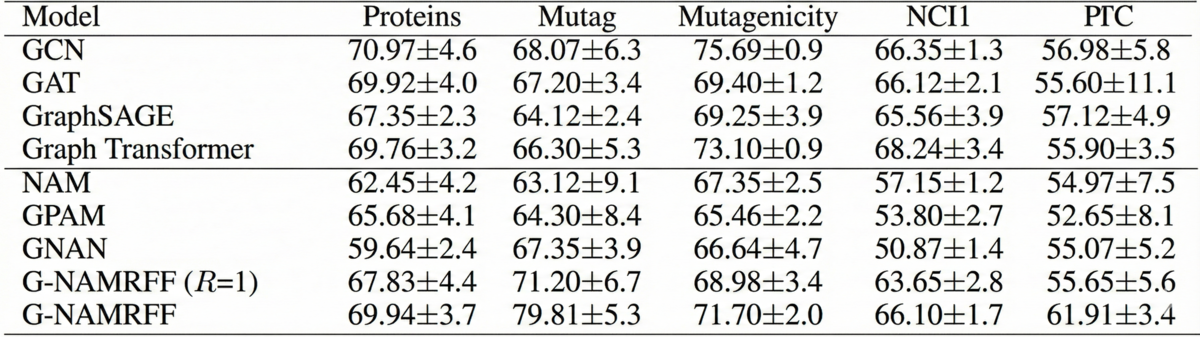
最先端のパフォーマンスとの比較:G-NAMRFFを、PubMedやCoraのような引用ネットワークからogbn-arxivのような大規模データセットまで、多様なベンチマークでテストしました。結果は決定的でした。私たちの解釈可能なアーキテクチャは、グラフ畳み込みネットワーク(GCN)やグラフアテンションネットワーク(GAT)のような主要な「ブラックボックス」モデルの精度に匹敵し、多くの場合、それを上回りました。これにより、予測能力を損なうことなく厳密な透明性を達成できることが証明されました。
フィルター次数からの洞察: 生の精度だけでなく、アブレーションスタディ(モデルの効いている要素を検証するための実験)では、モデルが学習する際の興味深い挙動が明らかになりました。学習された有限インパルス応答(FIR)フィルターを分析することで、モデルがより近い隣接ノードからの情報を優先しながらも、遠いノードからの必要なコンテキストを集約するように自動的に学習することを確認しました。
結論
このブログでは、信頼できるAIの2つの重要な側面、すなわち複雑なブラックボックスモデルの予測を説明することと、最初から透明な新しいアーキテクチャを設計することについて説明しました。 私たちの説明可能性フレームワークは、組織全体で多様なGNNを監査および理解する柔軟性を提供し、コンプライアンスを確保し、モデルのデバッグを支援します。これを補完する自己解釈可能アーキテクチャG-NAMRFFは、高性能と透明性が自然に共存する次世代のグラフAIへの道を開きます。私たちの研究室では、詐欺検出、信用スコア割り当てなど、実世界で複雑なグラフタスクを解決するためにこれらの技術を継続して使用しています。
これらの技術について詳しく知りたい方は、ぜひお問い合わせください!皆様からのご意見をお待ちしております!
参考文献
[1] Wang, Xiang, et al. "Reinforced causal explainer for graph neural networks." IEEE Transactions on Pattern Analysis and Machine Intelligence 45.2 (2022): 2297-2309.
[2] Numeroso, Danilo, and Davide Bacciu. "Meg: Generating molecular counterfactual explanations for deep graph networks." 2021 International Joint Conference on Neural Networks (IJCNN). IEEE, 2021.
[3] Wang, Xiaoqi, and Han-Wei Shen. "Gnninterpreter: A probabilistic generative model-level explanation for graph neural networks." arXiv preprint arXiv:2209.07924 (2022).
[4] Azzolin, Steve, et al. "Global explainability of gnns via logic combination of learned concepts." arXiv preprint arXiv:2210.07147 (2022).
[5] Agarwal, Rishabh, et al. "Neural additive models: Interpretable machine learning with neural nets." Advances in neural information processing systems 34 (2021): 4699-4711.
[6] Rahimi, Ali, and Benjamin Recht. "Random features for large-scale kernel machines." Advances in neural information processing systems 20 (2007).
[7] Bechler-Speicher, Maya, Amir Globerson, and Ran Gilad-Bachrach. "The intelligible and effective graph neural additive network." Advances in Neural Information Processing Systems 37 (2024): 90552-90578.
[8] Kazius, Jeroen, Ross McGuire, and Roberta Bursi. "Derivation and validation of toxicophores for mutagenicity prediction." Journal of medicinal chemistry 48.1 (2005): 312-320.