Please enable JavaScript in your browser.

fltech - 富士通研究所の技術ブログ

富士通研究所の研究員がさまざまなテーマで語る技術ブログ

Top > ICML > ICML2024 にて「アクション説明を考慮した決定木および木アンサンブルの学習技術」について発表します

ICML2024 にて「アクション説明を考慮した決定木および木アンサンブルの学習技術」について発表します

ICML ML AI 論文解説

はじめに

こんにちは．人工知能研究所の金森です． 富士通研究所では「説明可能AI（XAI）技術を用いた意思決定支援」に関する研究開発を行っており，現実世界の意思決定タスクへの適用（例えば，エンゲージメント調査データに基づいた従業員の生産性向上アクションの発見）に取り組んでいます． このたび，我々の研究成果である「アクション説明を考慮した決定木および木アンサンブルの学習技術」に関する研究論文が，機械学習分野の主要な国際会議である ICML2024 に spotlight 論文（投稿論文の上位3.5%！） として採択されたので，その内容を紹介します．

対象論文

採択された論文の内容

ひとこと概要

本論文では，機械学習モデルとして決定木および木アンサンブルモデルに，機械学習モデルの説明技術として反実仮想説明に基づくアクション説明技術にそれぞれ着目し，高精度な予測と現実的なアクション説明を両立したモデルを効率よく学習する方法を提案しました．

背景

反実仮想説明に基づくアクション説明技術とアルゴリズム的償還

深層学習技術や基盤モデル，そして生成AIに代表されるAI技術の劇的な発展にともなって，機械学習モデルの予測を用いて様々な意思決定タスクを効率化するデータ駆動型意思決定の普及が進みつつあります．一方で，実社会の意思決定の局面では，ユーザが機械学習モデルの出力する予測結果を信頼して受容するために，予測結果についてなんらかの追加情報を提示できる 説明可能性（explainability） の実現が重要視されており，これまでに様々な説明技術が研究・提案されてきました [1]．

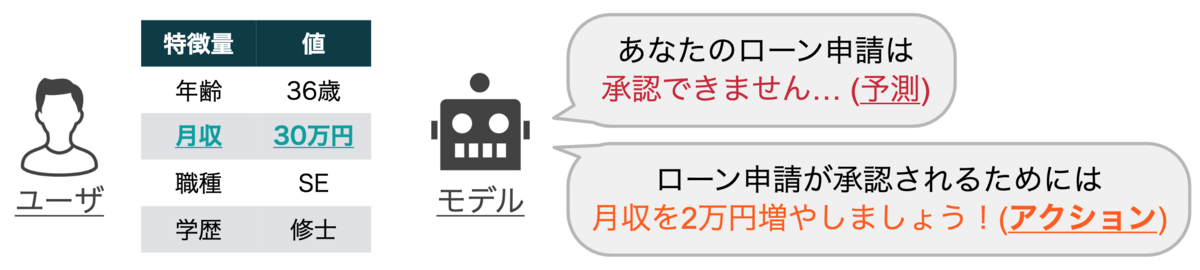
中でも 反実仮想説明法（counterfactual explanation）[2] は，「所望の予測結果を得るために必要な特徴量の変更方法（アクション）」を説明として提示する技術です．例えば，ユーザの月収や信用履歴などの情報を入力としてローン審査を行う機械学習モデルに対して反実仮想説明法を適用すると，「未返済のローン数を一つ減らす」や「月収を2万円増やす」などのようにローン審査を通過するためのアクションを説明として得ることができます（図１）．このように反実仮想説明法は，予測根拠などを提示する従来の説明技術と比較すると，アクションという形式で予測結果についてより建設的な説明を得ることができるため，近年注目されている説明技術の一つです [3]．

加えてこの反実仮想説明法は，AIの新しい信頼性の観点である アルゴリズム的償還（algorithmic recourse） を実現するための基盤技術としても重要視されています．これは，「ユーザ（人間）が適切な行動（アクション）をとれば，必ずAIから所望の結果を得られる」ということを保証する試みであり，その重要性から近年盛んに研究が行なわれています [4]．

図１．反実仮想説明に基づくアクション説明技術の例

既存技術の課題

反実仮想説明法に関する従来研究の多くは，既に学習済みのモデルからアクションを抽出する手法の開発に取り組んでいます．例えば我々のグループでもこれまでに，データ分布を考慮した現実的なアクション説明技術 [5] や，特徴量間の因果関係を考慮して実行順序を最適化するアクション説明技術 [6]，そしてユーザ集団に対して提示されるアクションを解釈可能な形で要約する説明技術 [7] を研究・開発してきました．

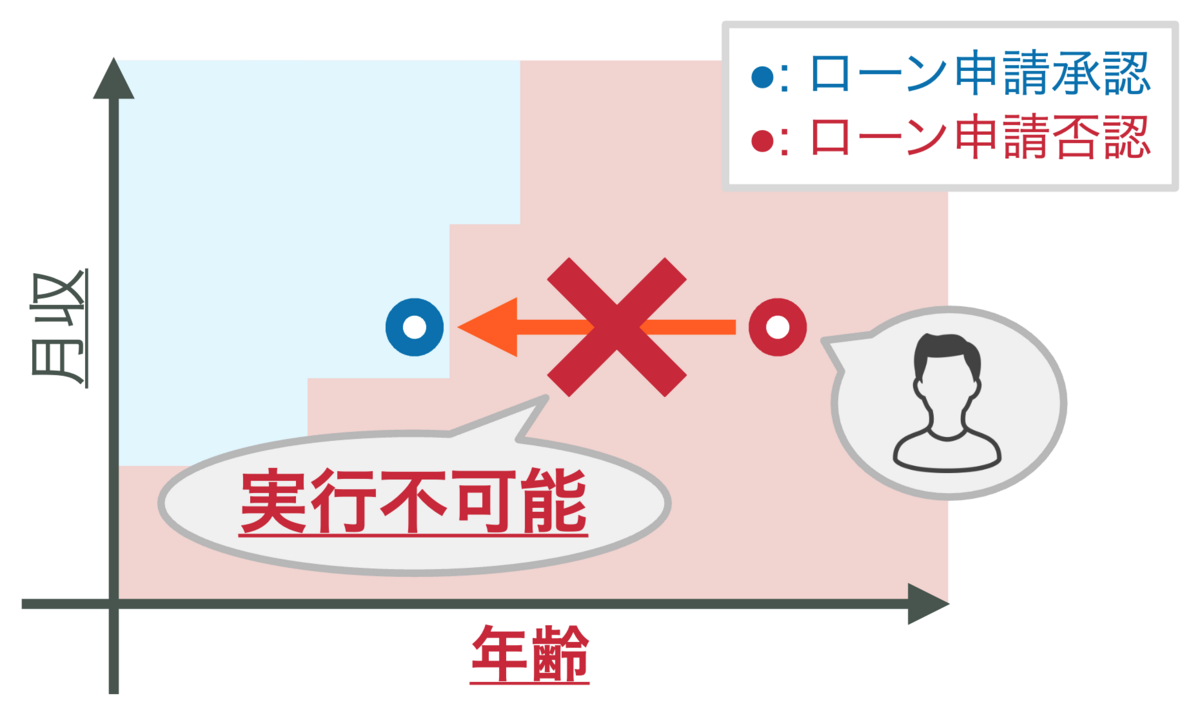
しかし，学習済みモデルに対して，そもそもユーザが実行可能でなおかつ所望の結果を得られるアクションが存在するとは限りません．具体例を図２に示します．図２は，「年齢」と「月収」という二つの特徴量から学習されたローン審査モデルの決定領域を示しています．ここでは，赤と青の領域がそれぞれ機械学習モデルがユーザのローン申請を拒否または許可と判定する領域に対応しています．いま，あるユーザの現在の特徴量値が特徴量空間上の点で表されており，赤の領域から青の領域への移動方法（どの特徴量をどのくらいの量だけ変更するか）がアクションに対応します．図２の機械学習モデルにおいて，ユーザは「年齢」という特徴量の値を減少させることで青の領域に移動することができますが，これは「若返る（！）」というアクションに相当するため，一般的には（？）実行不可能なアクションと言えます．一方で，「年収」という特徴量を増加させることはアクションとして妥当で十分実行可能に思えますが，図２を見る限り，このモデルに対してそのようなアクションを実行してもユーザは青の領域に移動することはできません．このように，主に予測精度のみを評価指標として学習されたモデルに対して，ユーザにとって現実的なアクションが常に存在する保証はありません．

この課題を解決するためには，各ユーザに対して有効なアクションが存在するかどうかをモデル学習時点で考慮しなければならないため，新しい学習の枠組みの開発が必要です．実はこの課題は Ross らによる先行研究 [8] で既に指摘されており，「アクション説明を考慮した学習技術」が提案されています．しかしこの既存技術は，深層学習モデルを前提とした勾配法ベースの学習アルゴリズムであり，アクション説明が重要視される予測タスク（ローン審査 など）で頻出する表形式データに対して広く用いられている決定木および木アンサンブルモデル（ランダムフォレスト [9] など）には適用することができませんでした．

図２．既存技術の課題のデモンストレーション

本論文の貢献

上記の背景と問題を踏まえて，本論文では，機械学習モデルとして決定木および木アンサンブルモデルに着目し，所望の予測結果が得られる現実的なアクションが存在する入力データの割合（アクション保証率）を考慮した決定木の効率よい学習技術を提案しました．具体的には，

  1. 標準的なトップダウン型の決定木学習アルゴリズムを拡張することで，アクション保証率を考慮した決定木の学習技術を提案 しました．加えて，提案アルゴリズムは標準的な決定木学習アルゴリズム（CART [10] など）と同等の時間計算量であることや，ランダムフォレストの枠組みにも容易に拡張可能であることを示しました．
  2. アクション保証率に関する制約の下で学習済み決定木を編集するタスクを新たに導入 し，このタスクが重み付き部分被覆問題という最小被覆問題の亜種に帰着できることを示しました．また，PAC学習の枠組みを用いて，テストデータに対するアクション保証率について確率的な理論保証を与えられることも示しました．
  3. 金融分野と司法分野における実データセットを用いた計算機実験を行い，提案手法により予測精度や学習速度を損なうことなくアクション保証率を大幅に向上できることを示しました．具体的には，予測精度劣化を1%程度に抑えつつ，アクション保証率を最大で50%ほど向上できた ことを確認しました．

以降で，必要な定義をいくつか導入した後，提案手法と結果の概略について紹介します．詳細については元論文をご参照いただけると幸いです．

技術的詳細

学習問題の定式化

決定木

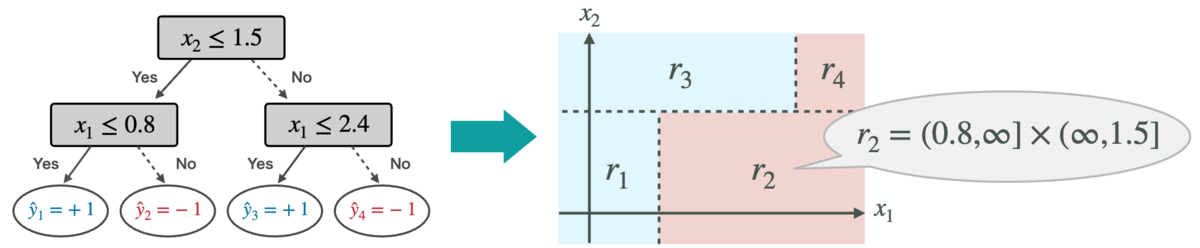
決定木（decision tree） は，"if-then-else" 形式のルール集合を二分木で表現した最もポピュラーな機械学習モデルの一つです．入力 x \in \mathbb{R}^D に対して決定木 h \colon \mathbb{R}^D \to \{ \pm 1 \} は，まず根ノードからスタートして，各中間ノードの 分岐条件 x_d \leq b に従って木を辿り，最終的に到達した葉ノードの 予測ラベル \hat{y} \in \{ \pm 1 \} を予測値として出力します．

所与の訓練データから決定木を学習するためには，木の構造と各中間ノードの分岐条件，そして各葉ノードの予測ラベルを決定する必要があります．しかし，訓練誤差を最小化する決定木を求める問題は計算量的に解くことが難しい組合せ最適化問題であるため，効率よく厳密解を得ることは困難です．そこで，CART [10] に代表される 貪欲法に基づくトップダウン型の学習アルゴリズム が広く用いられています．

図３．決定木の例

※ 弊社の決定木に関する研究については，以下の記事もご参照ください！

アクション説明

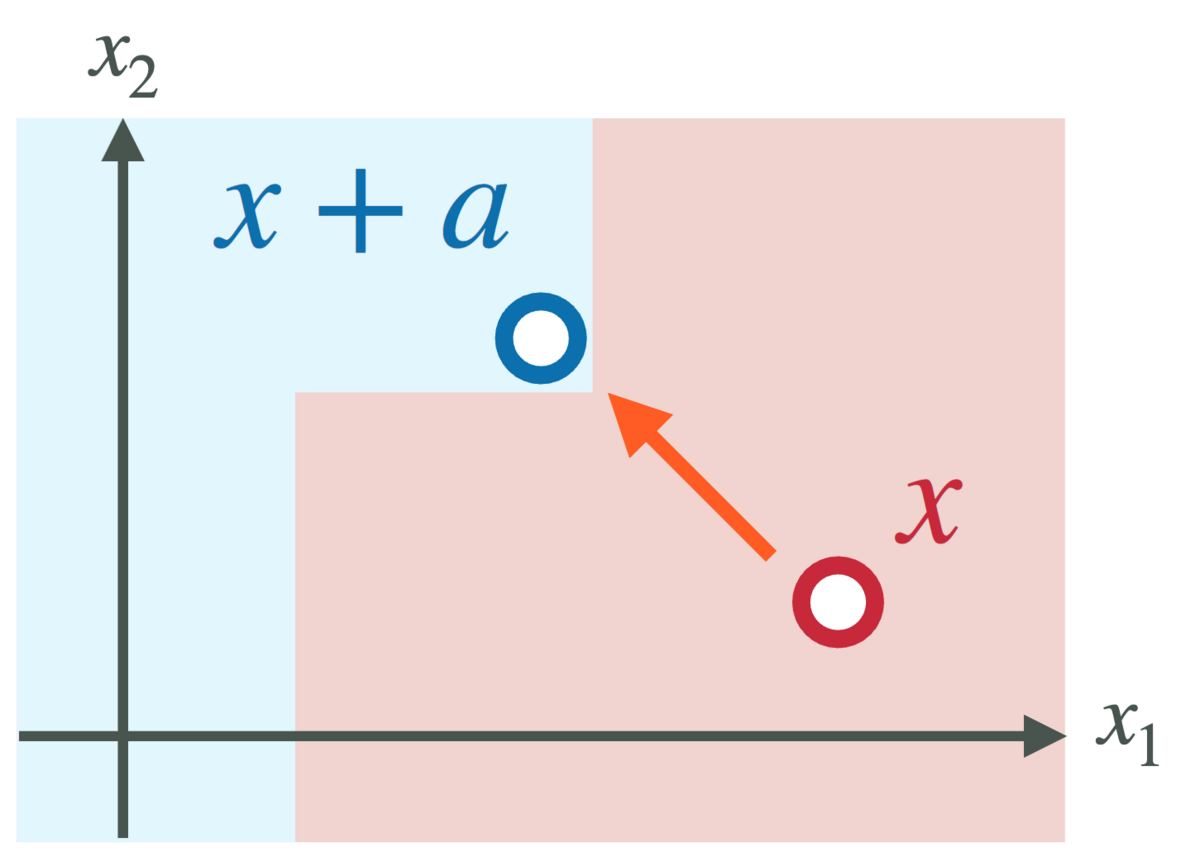
いま，所望の予測結果を y = +1 と仮定します．反実仮想説明法（counterfactual explanation）[2] に基づくアクション説明は，所与の入力 x \in \mathbb{R}^D とモデル h \colon \mathbb{R}^D \to \{ \pm 1 \} に対して，以下の最適化問題の最適解となる アクション a^\ast \in \mathbb{R}^D を求めます：

{\min}_{a \in \mathcal{A}} \; c(a) \;\;\; \text{subject to} \;\; h(x + a) = +1

ここで \mathcal{A} \subseteq \mathbb{R}^D は 実行可能アクション集合， c \colon \mathcal{A} \to \mathbb{R}_{\geq 0} はアクション a \in \mathcal{A} の実行コストを評価する コスト関数 です．

実行可能アクション集合の定義は予測タスクに依存しますが，ここでは \mathcal{A} = [ l_1, u_1 ] \times \dots \times [ l_D, u_D ] \subseteq \mathbb{R}^D の形で表現されることを仮定します．例えば年齢や性別などのように変更不可能な特徴量 d \in [ D ] については，対応する上下限の値を l_d = u_d = 0 と設定することで変更できないように制約することができます．

また，コスト関数は現実的なアクションを得るうえで重要な役割を果たすため，これまでに様々なコスト関数が提案されてきました．本論文では， c(a) = \max_{d \in [ D ]} c_d(a_d) の形で表現される \ell_{\infty}-ノルム型のコスト関数を仮定します（関数 c_d \colon \mathbb{R} \to \mathbb{R}_{\geq 0} は特徴量 d に関するコスト指標）．この形式のコスト関数は max percentile shift [4] などいくつかの主要コスト関数を含みます．

図４．アクション最適化問題の例

※ 弊社のアクション説明技術に関するこれまでの研究については，以下の記事もご参照ください！

学習問題の定式化

本論文の目標は，所望の予測結果が得られる現実的なアクションが存在する入力データの割合（アクション保証率）を考慮しつつ予測精度の高い決定木を効率よく学習することです．このために，まずアクション保証率を評価するための指標として 償還損失（recourse loss） を新たに導入します：

l_\mathrm{rec}(x; h) = \min_{a \in \mathcal{A}_{\varepsilon} } l_{01}(+1, h(x + a))

ここで l_{01}(y, \hat{y}) = \mathbb{I}[y \not= \hat{y}] は0-1損失関数， \mathcal{A}_{\varepsilon} = \{ a \in \mathcal{A} \mid c(a) \leq \varepsilon \} は コスト予算つきアクション集合 で，コストが所与の閾値 \varepsilon > 0 以下の実行可能アクションの集合です．導入した償還損失関数は，入力 x とモデル h に対して，所望の予測結果が得られて（つまり， h(x + a) = +1）なおかつ現実的（つまり， a \in \mathcal{A} かつ c(a) \leq \varepsilon）なアクションが存在する場合は 0 を，そうでなければ 1 をとります．この償還損失の訓練サンプル S = \{ (x_n, y_n) \}_{n=1}^{N} 上での平均値 \hat{\Omega}_{\varepsilon}(h) = \frac{1}{N} \sum_{n=1}^{N} l_\mathrm{rec}(x_n; h) を 経験償還損失（empirical recourse risk） として定義することにします．定義より，経験償還損失は「所望の予測結果が得られる現実的なアクションが存在しない訓練サンプルの割合」と解釈することができます．

経験償還損失を用いて，本論文の学習問題を以下のように定式化します：

{\min}_{h \in \mathcal{H}} \; \hat{R}(h) \;\;\; \text{subject to} \;\; \hat{\Omega}_{\varepsilon}(h) \leq \delta

ここで \mathcal{H} は決定木の集合， \hat{R}(h) = \frac{1}{N} \sum_{n=1}^{N} l_{01}(y_n, h(x_n)) は経験損失，そして \delta \geq 0 は所与のハイパーパラメータです．上記の学習問題を解くことで，訓練サンプル S において 100 \cdot (1 - \delta) \% 以上の入力 x に所望の予測結果が得られる現実的なアクション a の存在を保証しつつ，高精度な決定木 h を学習できる ことが期待されます．

提案アルゴリズム

前述の通り，決定木の学習問題は厳密に解くことが難しい組合せ最適化問題であり，貪欲法に基づくトップダウン型のアルゴリズムを用いることが主流です．標準的な学習アルゴリズムでは，分岐条件と予測ラベルを情報利得（大雑把に言うと，新たな分岐条件の追加によってどれだけ予測誤差を減少させることができるか）に基づいてトップダウンに決定していきます．

本論文の提案アルゴリズムは，この トップダウン型学習アルゴリズムを拡張 したシンプルなものです．いま，現在の決定木 h に新たな分岐条件 x_d \leq b を持つ中間ノードと予測ラベル \hat{y}_{\mathrm{L}}, \hat{y}_{\mathrm{R}} を持つ左右の葉ノードを追加することを考え，その決定木を h' で表すこととします．このとき提案アルゴリズムは，以下の評価指標を最小化するような分岐条件のパラメータ d \in [ D ], b \in \mathbb{R} と予測ラベル \hat{y}_{\mathrm{L}}, \hat{y}_{\mathrm{R}} \in \{ \pm 1 \} を決定します：

\Phi_\lambda(d, b, \hat{y}_{\mathrm{L}}, \hat{y}_{\mathrm{R}}) = \hat{R}(h') + \lambda \cdot \hat{\Omega}_{\varepsilon}(h')

ここで \lambda \geq 0 は所与のトレードオフパラメータです．評価指標 \Phi_\lambda の第2項 \lambda \cdot \hat{\Omega}_{\varepsilon}(h') は，元の学習問題における経験償還損失に関する制約 \hat{\Omega}_{\varepsilon}(h) \leq \delta の緩和とみなすことができます．各ノードにおいて上記評価指標 \Phi_\lambda を最小化する問題（分岐条件決定問題）を解くことで分岐条件 x_d \leq b と予測ラベル \hat{y}_{\mathrm{L}}, \hat{y}_{\mathrm{R}} を決定していき，この手続きを再帰的に繰り返すことでトップダウンに決定木を学習します．

図５．提案アルゴリズムの動作例

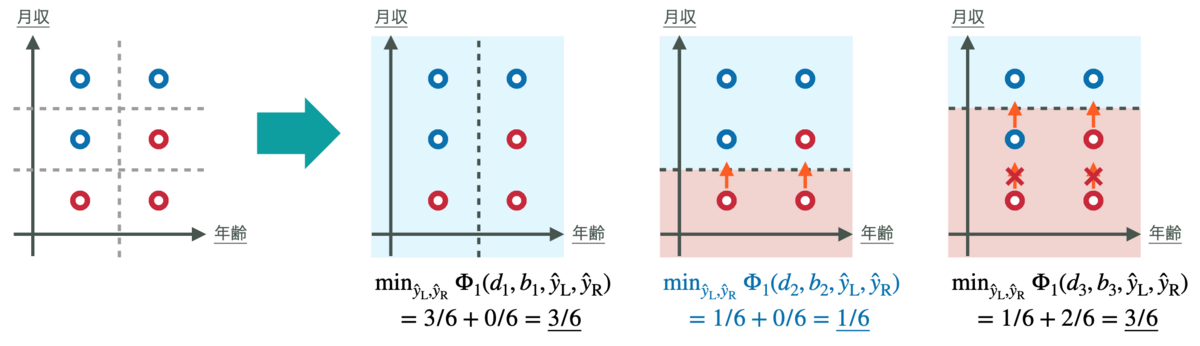
なお，提案手法は標準的な決定木学習アルゴリズムのシンプルな拡張であるため，代表的な木アンサンブルモデル学習法である ランダムフォレスト [9] の枠組みにも容易に適用可能 です．ランダムフォレストの学習アルゴリズムでは，特徴量サブサンプリングとバギングの併用により相異なる複数の決定木が学習されます．各決定木の学習における分割点決定アルゴリズムを提案アルゴリズムに置き換えることで，提案手法をランダムフォレストに拡張することができます．

理論的な結果

前述した通り，提案アルゴリズムは経験損失に加えて経験償還損失も考慮した評価指標のもとで分岐条件決定問題を解きます．ここで経験償還損失を無視（つまり \lambda = 0 に設定）すると，標準的な決定木の学習アルゴリズムが解いている分岐条件決定問題と概ね一致し，これは適切な前処理（訓練サンプルのソート など）をしておけば \mathcal{O}(D \cdot N) で解けることが知られています．本論文では，経験償還損失を考慮した場合（ \lambda > 0）でも同等の時間計算量で分割点決定問題が解けること（つまり，追加制約によるオーバーヘッドがないこと） を示しました（提案アルゴリズムの疑似コードについては元論文をご参照ください）．

Proposition 1.
提案アルゴリズムは経験償還損失を考慮した分岐条件決定問題（ \lambda > 0）を時間計算量 \mathcal{O}(D \cdot N) で解く．

一方で，提案アルゴリズムは元の学習問題の制約 \hat{\Omega}_{\varepsilon}(h) \leq \delta を緩和した指標のもとで決定木を学習するため，最終的に得られる決定木がこの制約を満たすとは限りません．そこで，学習済み決定木の葉ノードの予測ラベルをいくつかフリップすることで制約を満たすように編集するタスク（予測ラベル編集問題）を新たに導入します．本論文では，このタスクが 重み付き部分被覆問題（weighted partial cover problem）という最小被覆問題の亜種に帰着できる ことを示しました．重み付き部分被覆問題に対しては，近似率保証付きの多項式時間アルゴリズムが存在することが知られています．つまり，帰着した問題を解くことで，学習済みの決定木をアクション保証率に関する制約が満たされるように効率よく修正することができます．

Proposition 2.
予測ラベル編集問題は重み付き部分被覆に帰着される．

また，経験償還損失 \hat{\Omega}_{\varepsilon} は所与の訓練サンプル S 上でのアクション保証率を評価するものであり，未知のテストデータに対しても同じ確率でアクションの存在を保証できるとは限りません．本論文では，計算学習理論における基本的なテクニックである PAC学習（probability approximately correct learning） の枠組みを用いることで，経験償還損失の推定誤差の上界 を示しました．この結果を前述の予測ラベル編集問題と組合せることで，テストデータに対するアクション保証率についても理論的保証を与えられるようになります．

Proposition 3.
期待償還損失を \Omega_{\varepsilon}(h) = \mathbb{E}_{x} [l_\mathrm{rec}(x; h)] で定めると，任意の \alpha > 0 に対して確率 1 - \alpha 以上で次の不等式が成立: \Omega_{\varepsilon}(h) \leq \hat{\Omega}_{\varepsilon}(h) + \sqrt{\frac{\ln |\mathcal{H}| - \ln \alpha}{2 \cdot |S| }}

実験的な結果

計算機実験では，説明可能性分野でベンチマークとして広く用いられている４つの表形式データセット（FICO，COMPAS，Credit，Bail）上でベースライン手法との比較を行いました．ここで FICO と Credit は金融分野におけるローン審査に関する実データセットで，COMPAS と Bail は司法分野における再犯予測に関する実データセットです．ベースライン手法として，制約なしの標準的な学習法（Vanilla）と，アクションで変更可能な特徴量のみを用いる学習法（only actionable features; OAF）を用いました．各データセットにおいて10分割交差検証を行い，予測精度とアクション保証率，計算時間を計測しました．

図６．ベースライン比較実験の結果

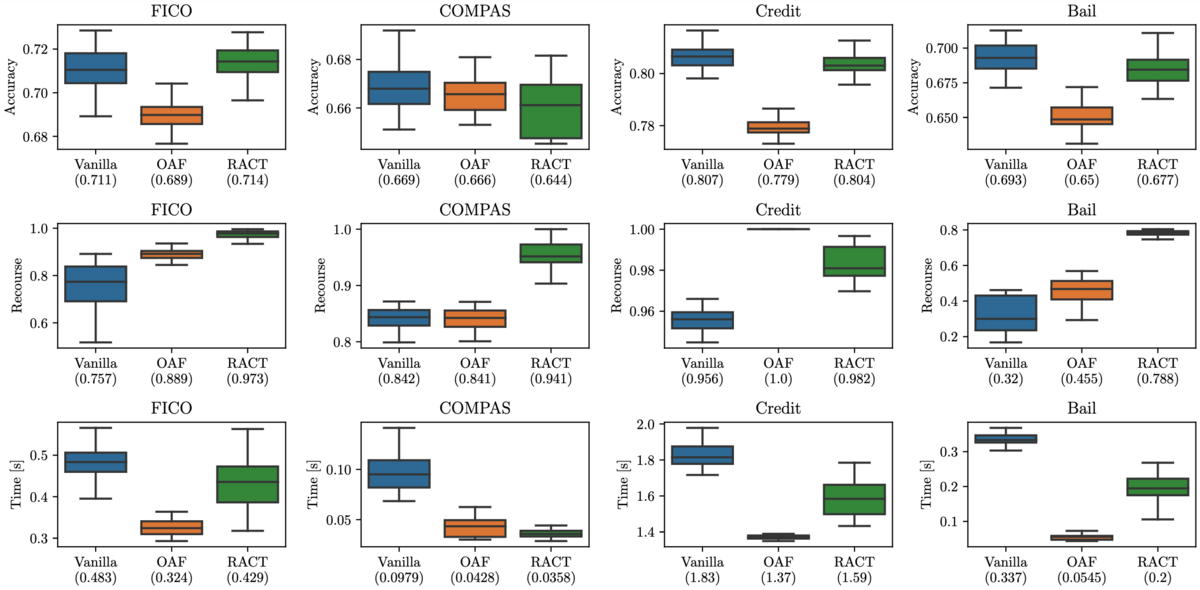
図６がベースラインとの比較実験の結果です．上段に予測精度，中段にアクション保証率，下段に計算時間をそれぞれ示しています．実験結果から提案手法（recurse-aware classification tree; RACT）は，ベースライン手法と比較して高いアクション保証率を達成できていることがわかります．一方で予測精度と計算時間については，手法間で大きな差はありませんでした．以上の結果から，提案手法（RACT）は予測精度と計算速度を損なわずに高いアクション保証率を実現できた ことを確認しました．

図７．トレードオフパラメータ \lambda の感度分析結果

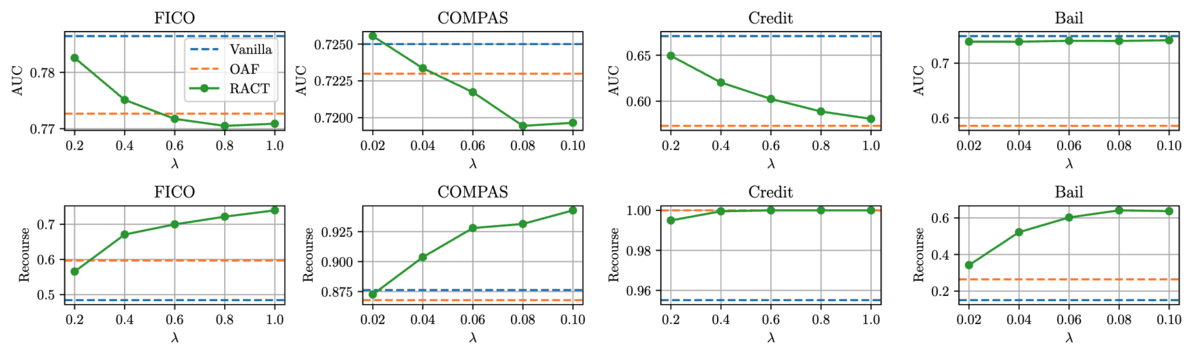
図７はランダムフォレストにおけるトレードオフパラメータ \lambda の感度分析に関する実験結果です．パラメータ \lambda の値が小さくなるほど AUC (上段) が, 大きくなるほどアクション保証率 (下段) が改善していることがわかります．この結果から，提案手法はトレードオフパラメータ \lambda を制御することで予測精度とアクション保証率のトレードオフを調整可能 であることが確認できます．実際の意思決定の局面において，予測精度を犠牲にしてまですべてのユーザにアクションを保証することが必ずしも要求されるとは限りません．この実験結果は，提案手法がそのような現実的なユースケースにも柔軟に対応可能であることを示唆していると言えます．

おわりに

本記事では，ICML2024 に spotlight 論文として採択された「アクション説明を考慮した決定木および木アンサンブルの学習技術」に関する研究について紹介しました．今後の課題としては，もう一つの代表的な木アンサンブルモデル学習フレームワークである勾配ブースティング（XGBoost や LightGBM）への拡張が挙げられます．また，実際の意思決定タスクへの適用も今後の課題の一つです．

参考文献

  • [1] 原 聡. 説明可能AI (私のブックマーク). 人工知能, Vol. 34, No. 4, pp. 577–582, 2018.
  • [2] S. Wachter, B. Mittelstadt, and C. Russell. Counterfactual explanations without opening the black box: Automated decisions and the GDPR. Harvard Journal of Law & Technology, Vol. 31, No. 2, pp. 841–887, 2018.
  • [3] 金森 憲太朗, 高木 拓也. 説明可能な機械学習のための数理最適化―混合整数線形最適化に基づく反実仮想説明法―. 応用数理, vol. 33, No. 4, pp. 207-212, 2023.
  • [4] B. Ustun, A. Spangher, and Y. Liu. Actionable recourse in linear classification. In Proceedings of the 2019 Conference on Fairness, Accountability, and Transparency (FAT* 2019), pp. 10–19, 2019.
  • [5] K. Kanamori, T. Takagi, K. Kobayashi, and H. Arimura. DACE: Distribution-aware counterfactual explanation by mixed-integer linear optimization. In Proceedings of the 29th International Joint Conference on Artificial Intelligence (IJCAI 2020), pp. 2855–2862, 2020.
  • [6] K. Kanamori, T. Takagi, K. Kobayashi, Y. Ike, K. Uemura, and H. Arimura. Ordered counterfactual explanation by mixed-integer linear optimization. In Proceedings of the 35th AAAI Conference on Artificial Intelligence (AAAI 2021), pp. 11564–11574, 2021.
  • [7] K. Kanamori, T. Takagi, K. Kobayashi, and Y. Ike. Counterfactual explanation trees: Transparent and consistent actionable recourse with decision trees. In Proceedings of the 25th International Conference on Artificial Intelligence and Statistics (AISTATS 2022), pp. 1846–1870, 2022.
  • [8] A. Ross, H. Lakkaraju, and O. Bastani. Learning models for actionable recourse. In Proceedings of the 35th International Conference on Neural Information Processing Systems (NeurIPS 2021), pp. 18734–18746, 2021.
  • [9] L. Breiman. Random forests. Machine Learning, Vol. 45, No. 1, pp. 5–32, 2001.
  • [10] L. Breiman, J. H. Friedman, R. A. Olshen, and C. J. Stone. Classification and Regression Trees. Wadsworth, 1984.