ICLR 2024で"Selective Mixup Fine-Tuning for Optimizing Non-Decomposable Objectives"について発表しました

こんにちは。AIイノベCPJの竹森です。富士通研究所とインド理科大学院(Indian Institute of Science)との共同研究において、画像分類タスクなどのための、複雑だが実用上重要な評価指標の効率的な最適化を可能にするAI技術を開発し、ICLR 2024 でspotlightとして発表したので、この技術ブログで発表内容について解説します。

採択論文

タイトル: Selective Mixup Fine-Tuning for Optimizing Non-Decomposable Objectives
国際会議: The Twelfth International Conference on Learning Representations (ICLR 2024)
著者: Shrinivas Ramasubramanian (FRIPL), Harsh Rangwani (IISc), Sho Takemori (FRJ), Kunal Samanta (IISc), Yuhei Umeda (FRJ), Venkatesh Babu Radhakrishnan (IISc)
論文へのリンク

(ここで、IIScはIndian Institute of Science, FRIPLはFujitsu Research of India Private Limited, FRJはFujitsu Research Japanの略です)。

動機付けと問題設定

この論文では、教師ありと半教師ありの両方の設定で動作する、分解不可能な指標を最適化するためのファインチューニング技術を提案しています。目的やなぜこのような問題を考えるのか、また用語の定義などについて以下で説明していきます。

クラス不均衡なデータセットと分解不可能な指標

画像分類タスクのための深層学習を用いた分類器にとって、精度(accuracy、正解率)は最も単純な評価指標ですが、実応用上はクラスラベルが不均衡であることがあります。そのような場合には、精度は適切な指標ではなく、F1やクラスごとに重みを付けた精度(balanced accuracy)などより複雑な指標の最適化を考えるほうがより適当です。この論文では、分解不可能な指標[Narasimhan et al., 2022]と呼ばれる分類問題のための複雑な指標(のクラス)の最適化を考えています。ここで、分類のための指標が分解可能とは、分類器が与えられたときに、各データのインスタンスに対してスコアが定義されていて、テストデータでの指標の値が各スコアから計算できるときに言います。そうでないときに、指標は分類不可能と呼ばれます。精度は分解可能な指標の例であり、F1やAUCは分解不可能な指標の例になっています。また、クラス不均衡なデータセットでは、頻度が少ないクラスでの精度を考慮するために、クラスごとにリコール(再現率)を定義し、それらのリコールの最小値の最大化を考えることがあります[Narasimhan and Menon, 2021]。より具体的には、この論文では、分類器 $h$ (またはスコア関数 $h$ )に対し、分類器の混同行列 $C[h]$ の関数として書ける(混同行列に対し定義された関数 $\psi$ があり指標が $\psi(C[h])$ として書ける)ことを仮定します。以下の表に、混同行列の関数としての分解不可能な指標の例を挙げます。ここでは、分類器のカバレッジ制約(分類器がクラス $i$ を予測する確率が閾値以上という制約。公平性に役立つ)を考えていますが、ラグランジュ乗数を導入して、制約なしの指標に帰着しています。ここで、表のmean recall, min recall, H-meanはそれぞれクラスごとのリコールの平均、最小値、調和平均を表し、いずれもクラス不均衡のための指標です。

特徴量抽出器により定義される分類器

以前の私たちの研究[Rangwani et al., 2022]でも、(半教師あり学習の設定で)分解不可能な指標の最適化を可能にする技術(Cost Sensitive Self-Training, CSST)を提案していましたが、CSSTは深層ニューラルネットワークモデルをフルスクラッチで学習する必要があり、計算効率性の点で課題がありました。また、既存研究により、クラス不均衡の場合には、特徴量抽出器と最終層の線形分類器を別々に学習したほうが、良い性能が得られることが知られています([Zhong et al., 2021]など)。そこで本論文では、特徴量抽出器 $g$ が与えられたときに、最終層の線形分類器を学習する"selective mixup"と呼ばれるファインチューニング技術を提案します。Mixupの定義などは、後で与えることにして、分類器に関する仮定を記号を使って説明します。 $K$ をクラスラベル数とし、 $\mathcal{X}$ をインスタンスの空間(画像の集合)とします。分類器 $F:\mathcal{X} \rightarrow [K]$ は、スコア関数 $h$ によって、 $F(x) = \mathrm{argmax}_i h_i(x)$ と与えられると仮定し、さらにスコア関数は、行列 $W\in \mathbb{R}^{d\times K}$ によって決まる最終層の線形分類器と特徴量抽出器 $g : \mathrm{X} \rightarrow \mathbb{R}^{d}$ によって、 $h(x) = W^{T} g(x)$ 　と書けると仮定します。

半教師あり学習と教師あり学習

以前の私たちの研究[Rangwani et al., 2022]のように、提案手法はラベルのないインスタンスを活用できます(つまり、半教師あり学習手法)。本論文の主な主眼は、半教師あり学習の設定ですが、提案手法は容易に教師あり学習の設定に拡張でき、以下で教師あり学習の設定の実験結果も紹介します。

提案手法

Feature mixupと (i, j)-Mixup

Mixupは、データ増強(data augmentation)手法であり、既存研究によって(主にクラス不均衡の問題がない標準的な設定において)、mixupにより分類器がより良い汎化性能、キャリブレーション、ロバスト性をもつことが知られています[Zhang et al., 2018, Zhang et al., 2021, Zhong et al., 2021]。最も基本的な場合には、mixupは２つのサンプル $(x, y), (x', y') \in \mathcal{X} \times \mathbb{R}^{K}$ に対し、凸結合により新しいサンプルを作ります。具体的には、 $\beta \in (0, 1)$ として、新しいサンプルを $(\beta x + (1 -\beta)x', \beta y + (1 - \beta)y')$ と定義します。ここで、クラスラベルと $\mathbb{R}^{K}$ のone-hot vectorを同一視しています。 Mixupは変種がいくつか提案されていますが、私たちの提案手法は、feature mixup [Verma et al., 2019]をもとにしていて、インスタンス $x$ ではなく、特徴量空間での凸結合 $\beta g(x) + (1 - \beta)g(x')$ を考えます。２つのサンプル $(x, y), (x', y')$ 　に対して、mixup損失関数を

$\mathcal{L}_{mixup}(g(x), g(x'), y; W) = \mathcal{L}_{SCE}(W^{T} (\beta g(x) + (1 -\beta) g(x')), y),$

と定義します。ここで、 $\mathcal{L}_{SCE}$ はクロスエントロピー損失関数(softmax cross entropy)を表します。

通常のmixupは、２つのサンプルをランダムに選びますが、私たちの設定ではクラス不均衡の問題があり、また複雑な指標の最適化を目的としているので、ランダムに選択すると良い性能が得られなくなります。そこで、２つのサンプルのクラスラベルを考慮した (i, j)-mixupというものを考えます。２つのサンプル $(x, y)$ , $(x', y')$ に対して、 $y = i, y' = j$ の時、feature mixup $(\beta g(x) + (1 -\beta)g(x'), y)$ を (i, j)-mixupと呼びます。ここでは、mixupされたサンプルのクラスラベルを $y$ としています。各クラスラベル $y \in [K]$ 　に対し、 $D_y \subset \mathcal{X}$ でクラスラベル $y$ に属するインスタンスの部分集合を表します。半教師あり学習の設定では、 $\widetilde{D}_y$ で疑似ラベル $y$ を持つインスタンスの集合とします。ベクトル $z_y$ 　で、 $D_y$ 　に属する平均特徴量ベクトル $\mathbb{E}_{x \sim D_y}[g(x)]$ を表すとき、 (i, j)-mixupによる損失関数を、以下で定義します。

$\mathcal{L}^{mix}_{(i, j)} = \mathcal{L}_{mixup}(z_i, z_j, i; W).$

(i, j)-mixup による指標の変化

(i, j)-mixupを適用したとき、最終層の線形分類器を定義する行列 $W$ を損失関数の勾配 $V_{ij}:= -\partial{\mathcal{L}_{(i,j)}^{mix}}/{\partial{W}}$ を用いて更新します。この更新により、指標 $\psi(C[h])$ がどのように変化するかを近似的に述べます。 $\eta > 0$ を小さなスカラーとし、Taylor展開により以下が成立します。

$\psi(C[W^{T} g + \eta V_{ij}^{T} g])=\psi(C[W^{T} g]) + \eta \nabla_{V_{ij}}\psi(C[W^{T} g]) + O(\eta^{2} |V_{ij}|^{2}).$

ここで、 $\nabla_{V_{ij}}$ は方向微分を表します。 (i, j)-mixupによる gain　(指標の変化) を以下で定義します. $G_{ij} = \partial_{V_{ij}}\psi(C[W^{T} g]), \quad V_{ij}= -\partial{\mathcal{L}_{(i,j)}^{mix}}/{\partial{W}}.$

Selective Mixup

次にどのようにmixupのためのペア (i, j) を選ぶかを説明します。 $[K] \times [K]$ 上の確率分布 $\mathcal{P}$ があり、 $\mathcal{P}$ 　に従って、(i, j)を選択するとします。このとき、行列の変化の期待値は ( $\eta$ を無視すると)、 $V = \sum_{i, j} \mathcal{P}(i, j)V_{ij}$ と与えられ、(線形近似を行っているので)、指標の変化の期待値は、以下で与えられます。 $\mathbb{E}(G) = \sum_{i, j \in [K]\times [K]} \mathcal{P}(i, j)G_{ij}.$

gainの最適化のため、以下の分布を定義します(ここで s はinverse temperature parameter)。(i, j)-mixup を指標の値により適応的に選択するので、selective mixupと呼んでいます。 $P_{selmix}(i, j) = softmax ( s G_{ij})_{1 \le i, j \le K}.$

アルゴリズムの概要

Selective mixupを用いたアルゴリズムの概略を示します。各iteration $t=1,\dots, T$ 　に対して、SelMix分布 $\mathcal{P}_{selmix}^{(t)}$ 　を近似式を用いて計算し、クラスラベル $(Y_1, Y_2)$ を分布からサンプリングします。インスタンス $X_1, X_2$ を $\mathcal{D}_{Y_1}$ と $\mathcal{D}_{Y_2}$ から一様ランダムにサンプリングし、mixup損失関数 $\mathcal{L}_{mixup}$ の勾配を用いて、 $W$ を更新します。

理論的な結果

手法の収束性に関する理論的な結果を簡単に紹介します。理論解析の設定では、各iteration $t \ge 1$ に対して、アルゴリズムが mixup　pair $(i, j)$ をSelMix分布から選び、行列　 $W$ 　を $W^{(t + 1)} = W^{(t)} + \eta_t \widetilde{V}^{(t)}$ 　と更新します。ここで、 $\widetilde{V}^{(t)}$ は正規化された勾配 $V_{ij}/|V_{ij}|$ であり、 $\psi(C[W^{T} g])$ は $W$ に関して $\gamma$ -smoothで、concaveと仮定しています。さらに、 $\widetilde{V}^{(t)}$ は以下の仮定を満たすとします。定数 $c>0$ が存在し、 $\mathbb{E}[\widetilde{V}^{(t)}] \cdot \partial{\psi(W^{(t)})}/\partial{W} > |\partial{\psi(W^{(t)})}/\partial{W}|$ が全ての $t$ 　について成立する。また、 $W^{*}$ を最適なパラメータ $\mathrm{argmax}\psi(W)$ 　とします。追加の有界性の仮定などのもとで、標準的な議論から以下を示すことができます。

定理任意の $t > 1$ 　に対して、 $\psi(W^{*}) - \psi(W^{(t)}) = O(1/t)$ が成立する。

実験結果

提案手法を検証するため、半教師あり学習と教師あり学習の両方の設定で既存手法との比較を行います。ここでは簡単のため、CIFAR-10のクラス不均衡版であるCIFAR-10 LT (long-tailed)における実験結果を紹介します。他のデータセットでの実験結果などは、論文を参照してください。

半教師あり学習の設定

以下の実験では、上の表で紹介された、クラス不均衡なデータセット上での評価の際に重要な、最適化が困難な指標を評価指標としています。以下のグラフでは、提案手法(SelMix)とこの問題設定でのSoTAである既存手法と比較しています(CSST [Rangwani et al., 2022], DASO [Oh et al., 2022], ABC [Lee et al., 2021], logit-adjusted 損失関数と組み合わせたFixMatch [Sohn et al., 2020])。グラフから、提案手法が既存手法の性能を大きく上回っていることが分かります。

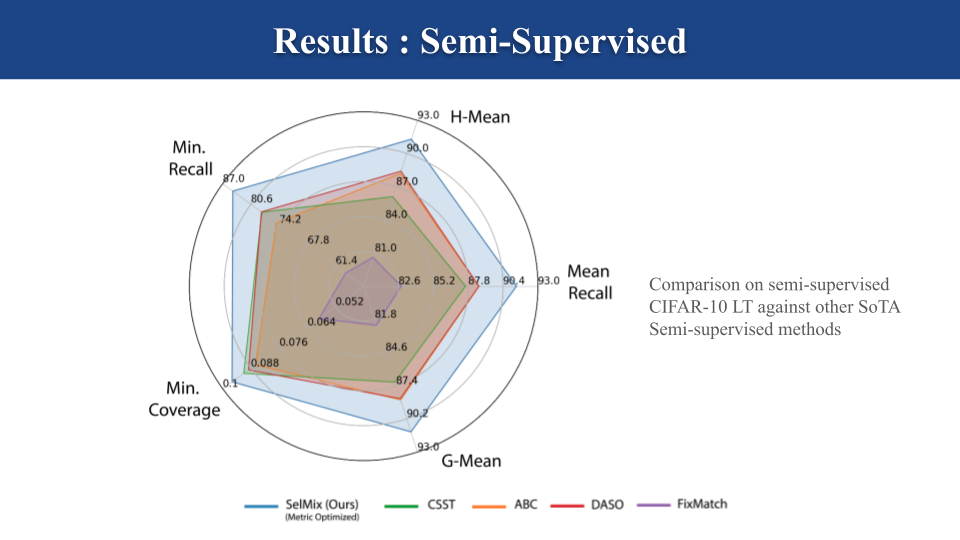
教師あり学習の設定

以下のグラフでは、教師あり学習の設定での実験結果を示しています。この設定でのベースラインは、SoTA手法のひとつである MiSLAS [Zhong el al., 2021] であり、MiSLASは学習過程を２つのステージ(特徴量抽出器の学習と線形分類器の学習(ファインチューニング))に分ける手法です。実験では、提案手法の特徴量抽出器にMiSLASのものを用いて、ファインチューニングの比較を行いました。この実験からも、提案手法が既存手法に優っていることが分かります。

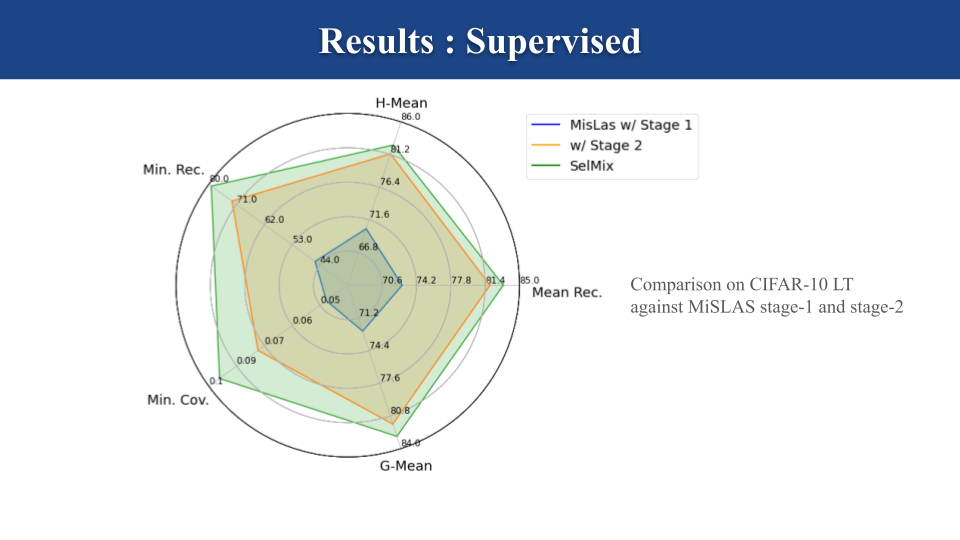
まとめ

私たちは、IIScと富士通研究所の共同研究において、分解不可能な指標の最適化を可能にするファインチューニング技術 SelMix を開発し、様々な実験条件で手法が有効であることを示しました。論文は、ICLR2024にspotlightとして採択され、共同研究の成果をICLR2024で発表しました。

References

Harikrishna Narasimhan and Aditya K Menon. Training over-parameterized models with nondecomposable objectives. Advances in Neural Information Processing Systems, 34, 2021
Harikrishna Narasimhan, Harish G Ramaswamy, Shiv Kumar Tavker, Drona Khurana, Praneeth Netrapalli, and Shivani Agarwal. Consistent multiclass algorithms for complex metrics and constraints. arXiv preprint arXiv:2210.09695, 2022.
Hyuck Lee, Seungjae Shin, and Heeyoung Kim. Abc: Auxiliary balanced classifier for classimbalanced semi-supervised learning. Advances in Neural Information Processing Systems, 34: 7082–7094, 2021.
Youngtaek Oh, Dong-Jin Kim, and In So Kweon. Daso: Distribution-aware semantics-oriented pseudo-label for imbalanced semi-supervised learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 9786–9796, 2022.
Kihyuk Sohn, David Berthelot, Nicholas Carlini, Zizhao Zhang, Han Zhang, Colin A Raffel, Ekin Dogus Cubuk, Alexey Kurakin, and Chun-Liang Li. Fixmatch: Simplifying semi-supervised learning with consistency and confidence. Advances in Neural Information Processing Systems, 33:596–608, 2020
Harsh Rangwani, Shrinivas Ramasubramanian, Sho Takemori, Kato Takashi, Yuhei Umeda, and Venkatesh Babu Radhakrishnan. Cost-sensitive self-training for optimizing non-decomposable metrics., Advances in Neural Information Processing Systems, 2022
Vikas Verma, Alex Lamb, Christopher Beckham, Amir Najafi, Ioannis Mitliagkas, David Lopez-Paz, and Yoshua Bengio. Manifold mixup: Better representations by interpolating hidden states. In International Conference on Machine Learning, pp. 6438–6447. PMLR, 2019.
L Zhang, Z Deng, K Kawaguchi, A Ghorbani, and J Zou. How does mixup help with robustness and generalization? In International Conference on Learning Representations, 2021.
Hongyi Zhang, Moustapha Cisse, Yann N Dauphin, and David Lopez-Paz. mixup: Beyond empirical risk minimization. In International Conference on Learning Representations, 2018.
Zhisheng Zhong, Jiequan Cui, Shu Liu, and Jiaya Jia. Improving calibration for long-tailed recognition. In IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 16489–16498, 2021

fltech - 富士通研究所の技術ブログ

富士通研究所の研究員がさまざまなテーマで語る技術ブログ