“Multi-Rate VAE: Train Once, Get the Full Rate-Distortion Curve” accepted at ICLR2023 as notable-top-5%

Recently, in our joint research with the University of Toronto, we have developed an AI technology called Multi-Rate VAE (MR-VAE), enabling the acquisition of the full rate-distortion curve by only a single training run. We will present our work at ICLR 2023 (notable-top-5%). In this blog post, we introduce our joint research.

Paper

Title: Multi-Rate VAE: Train Once, Get the Full Rate-Distortion Curve (Juhan Bae, Michael R. Zhang, Michael Ruan, Eric Wang, So Hasegawa, Jimmy Ba, Roger Baker Grosse)
Conference: The Eleventh International Conference on Learning Representations (ICLR 2023) openreview.net

Authors of this blog post: So Hasegawa, Juhan Bae

Overview

Introduction

Generative AI has become one of the popular topics in recent years, and generative models are the core of Generative AI. One of the key generative models is the Variational AutoEncoder (VAE) [Kingma, et al]. VAE consists of an encoder and a decoder, similar to AutoEncoder. The training process of VAE is encouraged to make a posterior of the encoder match a pre-determined prior. Fujitsu AI Laboratory has conducted research on a quantitative understanding of VAE and presented findings at ICML2020 [Kato, et al] and ICML2021 [Nakagawa, et al].

An objective function to train $\beta$ -VAE (a generalization of VAE) [Higgins, et al] consists of two terms: reconstruction error (distortion) and Kullback-Leibler divergence between the posterior distribution and prior one (rate) as the following formulation.

$\beta$ is KL weight that trades off distortion and rate. Multiple rounds of training with different $\beta$ values produce the rate-distortion curve (Fig 1.).

As shown in Fig 1, rate and distortion have the trade-off property, and the rate-distortion curve has two areas to denote.

Low distortion and high rate. The trained models reconstruct data with high quality and would generate unrealistic data
Low rate and high distortion. The trained models generate variational data in accordance with the prior distribution and would fail to reconstruct data

Practitioners often train $\beta$ -VAE multiple times with different $\beta$ s and evaluate these trained models in order to obtain the optimal rate and distortion depending on the task. If they use a simple neural network, the overall cost of multiple trainings can be ignored. However, if the model size is big, the entire cost becomes tremendous. Hence, the question comes to our mind. Can we obtain the rate-distortion curve in a single training run? The paper accepted at ICLR2023 proposes a solution to answer the question. The proposed method is able to save the cost of tuning $\beta$ . Moreover, we will show that the proposed method is significantly robust to the choice of $\beta$ with respect to various evaluation metrics.

Method

First, we introduce a response function that is the core topic of our method. The response function maps a set of hyperparameters to optimal model parameters trained with such hyperparameters. In the case of VAE, the response function maps $\beta$ to the optimal encoder and decoder parameters that minimize the $\beta$ -VAE objective. Our Multi-Rate VAE (MR-VAE) constructs the parametric response function by scaling the weight and bias of each VAE layer as in Fig 2.

Concretely, consider the $i$ -th layer of VAE, whose weight and bias are represented as $\rm{W}^{(i)} \in \mathbb{R}^{m_{i+1} \times m_i}$ and $\rm{b}^{(i)} \in \mathbb{R}^{ m_{i+1} }$ , respectively. We directly model response functions with hypernetworks $\psi$ by parameterizing each weight and bias as follows:

where $\odot$ and $\odot_{\rm{row}}$ indicate elementwise multiplication and row-wise rescaling. Also, we define the elementwise activation function $\sigma^{(i)}$ as:

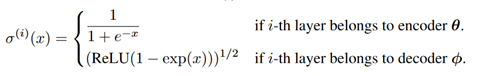
Please keep in mind that the proposed response function is memory and cost-efficient because it only requires $2m_{i}+1$ additional parameters and 2 additional elementwise multiplications for each layer during foward-pass. We can also show that the proposed response function recovers the exact response function for linear VAEs. Please refer to the appendix in our paper for the proof.

To acquire the optimal model parameters among various $\beta$ s, we propose an objective function of MR-VAE as:

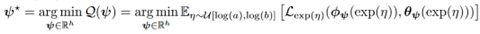
where $\mathcal{U} [\rm{log}(a), \rm{log}(b)$ ] is a uniform distribution with range $\rm{log}(a)$ and $\rm{log}(b)$ . It is analogous to the objective function of the Self-Tuning Network [Lorraine, et al][MacKay, et al][Bae, et al]. The objective function encourages response functions to learn optimal model parameters for various $\beta$ in a range between $a$ and $b$ .

Experiments

We would like to give answers to four fundamental questions regarding MR-VAE through experiments.

Can MR-VAE construct the rate-distortion curve in a single training run?
Can the hypernetwork be scaled to modern-size architectures?
How is MR-VAE sensitive to the sampling range of $\beta$ ?
How is MR-VAE applicable to other VAE models?

1. Can MR-VAE construct the rate-distortion curve in a single training run?

First, we need to validate our theoretical findings for MR-VAE on linear VAEs. MNIST is used as the dataset. We train MR-VAE on MNIST by sampling $\beta$ from 0.01 to 10.0. On the other hand, we train 10 separated linear VAEs with different values of $\beta$ . The rate-distortion curves acquired by the two models are shown in Fig 3. Clearly, the rate-distortion curve obtained by MR-VAE aligns with that gotten by linear VAEs.

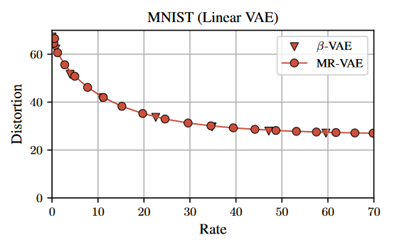
Fig 3: Rate-distortion curve by MR-VAE and Linear VAEs

2. Can the MR-VAE be scaled to modern-size architectures?

Next, we would like to ensure the versatility of our method with modern-size architectures and various datasets. We train Convolutional Neural Networks and ResNet-based architecture on binary static MNIST, Omniglot, CIFAR-10, SVHN, and Celeb-A. We also train NVAE [Vahdat, et al] on binary static MNIST, Omniglot, and CelebA. Finally, we train auto-regressive LSTM VAEs on the Yahoo dataset [He, et al]. The result is shown in Fig 4. The results highlight that our methods can learn competitive rate-distortion curves for various architectures and datasets.

Fig 4: Rate-distortion curve among various architectures and datasets

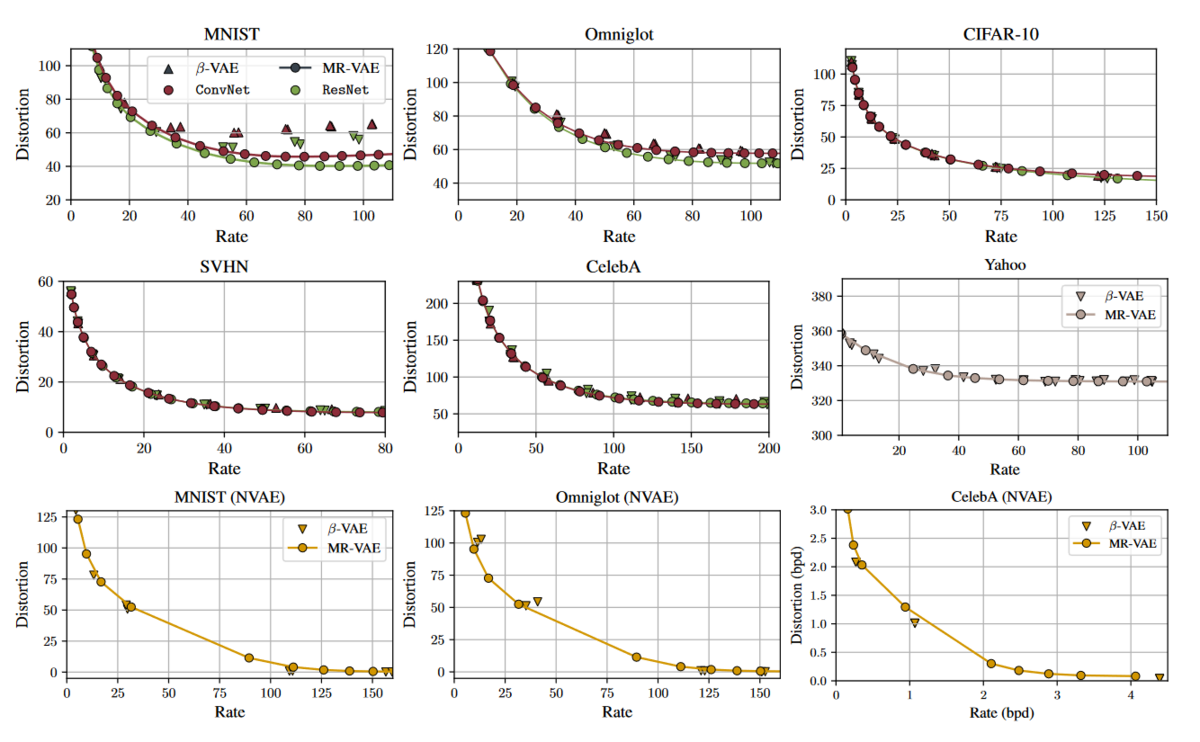
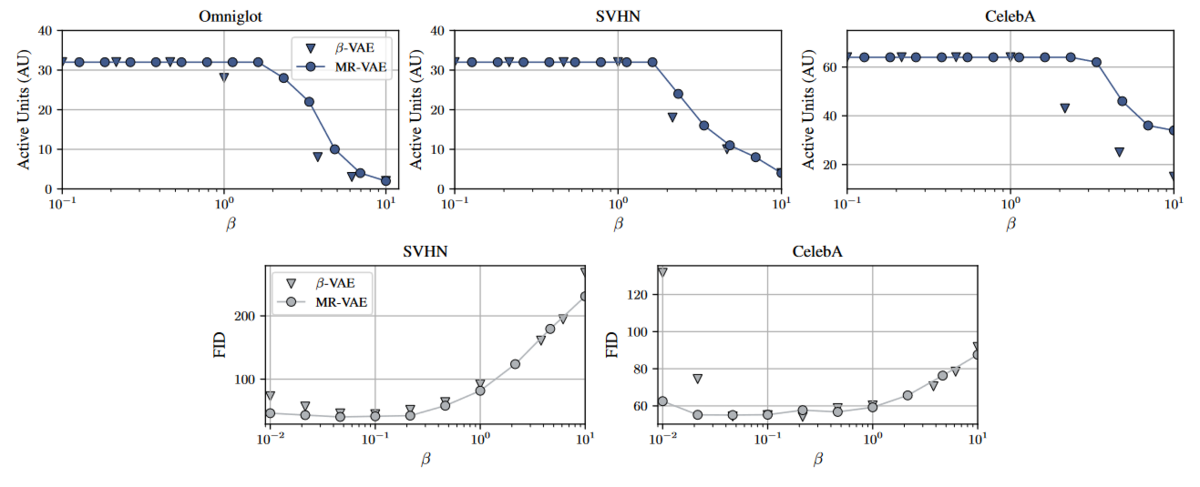
We also focused on the relationship between $\beta$ and various proxy metrics. We computed Fréchet Inception Distance [Heusel, et al] and Active Units [Burda, et al] for several datasets as in Fig 5. Interestingly, MR-VAE comes to acquire the meaningful latent variables (high Active Units) with high $\beta$ s and generate the more natural images (low FID) with low $\beta$ s. Sharing the parameters over some $\beta$ s would enable transferring learnt knowledge to other $\beta$ s. Likewise, we are able to obtain the intriguing results that MR-VAE is robust to FID and Active Units regardless of $\beta$ compared to conventional VAE.

3. How is MR-VAE sensitive to the sampling range of $\beta$ ?

MR-VAEs introduce two hyperparameters $a$ and $b$ . The two hyperparameters determine the range of sampling $\beta$ s during training. We train ResNet-based architecture on Omniglot and show the rate-distortion curves in Fig 6. On the left, we fixed $b$ = 10 and changed the sample range $a$ in the set {0.001, 0.01, 0.1, 1}, and on the right, we fixed $a$ = 0.01 and modified the sample range $b$ in the set {10, 1, 0.1}. While the length of the rate-distortion curves differs with different sample ranges, we observed that all the separated curves are consistent with each other.

Fig 6: MR-VAE under different sapling ranges of $β$

4. How is MR-VAE applicable to other VAE models?

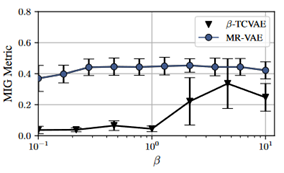
There are VAE models that make use of other objectives instead of reconstruction error and KL divergence. $\beta$ -TCVAE [Chen, et al] is the representative method that does not utilize KL divergence. Instead, $\beta$ in $\beta$ -TCVAE balances between the reconstruction error and the total correlation. We trained MR-VAEs consisting of MLP on the dSprites dataset. We compare $\beta$ -TCVAEs and MR-VAEs (trained with the $\beta$ -TCVAE objective) by examining their performance on the Mutual Information Gap (MIG) as in Fig 7. Intriguingly again, we observed that MR-VAEs are more robust to the choice of the $\beta$ and achieve better MIG performances than the baseline $\beta$ -TCVAEs.

Conclusion

We show Multi-rate VAE (MR-VAE), which is a method to produce the rate-distortion curve in a single training run. To achieve this, we introduced a simple memory and cost-efficient learnable response function. Across various modern-size architectures and tasks, MR-VAEs can acquire a competitive rate-distortion curve in a single training run. Moreover, we also showed that MR-VAE becomes more robust to the choice of $\beta$ with respect to various evaluation metrics (e.g., FID and Active Units).

In future research, we anticipate that the MR-VAE architecture could be extended to other generative models. Due to the difficulties with quantifying generation quality, generative models often exhibit trade-off properties (e.g., distortion and perception in super-resolution tasks [Blau, et al]). The property leads to training generative models multiple times with different hyperparameters and may require extensive training time, ranging from months to potentially years, particularly for large generative models prevalent today. We believe that the method proposed in our paper would be one of the potential solutions to address the problem.

Reference

Diederik P. Kingma, et al., “Auto-Encoding Variational Bayes”, International Conference on Learning Representations (ICLR), 2014
Keizo Kato, et al., “Rate-Distortion Optimization Guided Autoencoder for Isometric Embedding in Euclidean Latent Space”, International Conference on Machine Learning (ICML) 2020
Akira Nakagawa, et al., “Quantitative Understanding of VAE as a Non-linearly Scaled Isometric Embedding”, International Conference on Machine Learning (ICML) 2021
Irina Higgins, et al., “beta-VAE: Learning Basic Visual Concepts with a Constrained Variational Framework”, International Conference on Learning Representations (ICLR), 2017
Arash Vahdat, et al., “NVAE: A Deep Hierarchical Variational Autoencoder”, Neural Information Processing Systems (NeurIPS), 2020
Junxian He, et al., “Lagging Inference Networks and Posterior Collapse in Variational Autoencoders”, International Conference on Learning Representations (ICLR), 2019
Martin Heusel, et al., “Gans trained by a two time-scale update rule converge to a local nash equilibrium”, Neural Information Processing Systems (NeurIPS), 2017
Yuri Burda, et al., “Importance Weighted Autoencoders”, arXiv preprint arXiv:1509.00519, 2015
Ricky T. Q. Chen, et al., “Isolating Sources of Disentanglement in VAEs”, Neural Information Processing Systems (NeurIPS), 2018
Yochai Blau, et al., “The Perception-Distortion Tradeoff”, Computer Vision and Pattern Recognition Conference (CVPR), 2018
Jonathan Lorraine, et al. “Stochastic hyperparameter optimization through hypernetworks”, arXiv preprint arXiv:1802.09419, 2018
Matthew MacKay, et al., “Self-tuning networks: Bilevel optimization of hyperparameters using structured best-response functions”, arXiv preprint arXiv:1903.03088, 2019
Juhan Bae, et al., “Delta-stn: Efficient bilevel optimization for neural networks using structured response jacobians”, Neural Information Processing Systems (NeurIPS), 2020

fltech - 富士通研究所の技術ブログ

富士通研究所の研究員がさまざまなテーマで語る技術ブログ