“Automated Data Augmentation for Graph Classification” presented on ICLR 2023

We are conducting research about applying graph data augmentations to graph classification. Recently, we have completed a joint research project with Texas A&M University’s Data Integration, Visualization, and Exploration (DIVE) Laboratory (https://people.tamu.edu/~sji/), and the research paper titled “Automated Data Augmentations for Graph Classification”, has been accepted by ICLR 2023. This article briefly introduces our work in this research project.

Paper

Title: Automated Data Augmentations for Graph Classification (Youzhi Luo, Michael McThrow, Wing Au, Tao Komikado, Kanji Uchino, Koji Maruhashi, Shuiwang Ji)
Conference: Eleventh International Conference on Learning Representations (ICLR 2023) openreview.net

Overview

Many real-world data, such as financial transactions and molecular structures, can be naturally represented as graphs. Developing effective classification models for graph-structured data has been highly desirable but challenging. Recently, advances in deep learning have significantly accelerated the progress in this direction. Graph neural networks (GNNs), a class of deep neural network models specifically designed for graphs, have been widely applied to many graph classification tasks, such as fraud detection and molecular property prediction.

However, just like deep models on image and text, GNN models can easily overfit and fail to achieve satisfactory performance on small datasets. To address this issue, data augmentation can be used to generate more data labels or data samples. Data augmentation techniques have been widely used to reduce overfitting and improve robustness in training deep neural network models for image and text. While generating labels for unlabeled data is relatively straightforward for graph data, the reverse of generating data samples for a given label is not so.

An important property of desirable data augmentations is label-invariance, which requires that label-related information not be compromised during the augmentation process. This is easy for image data where commonly used image augmentations, such as flipping and rotation, can preserve almost all information of original images. However, graphs are non-Euclidean, so even minor structural modification of a graph can destroy important information in it. Currently, most existing graph augmentations are based on random modification of nodes and edges in the graph. Not being label-invariant, augmentations do not always improve the performance of graph classification models.

In this work, we propose GraphAug, a novel graph augmentation method that can produce label-invariant augmentations with an automated learning model. GraphAug uses a learnable model to automate augmentation category selection and graph transformations. It optimizes the model to maximize an estimated label-invariance probability through reinforcement learning. To our best knowledge, GraphAug is the first work successfully applying automated data augmentations to generate new graph data samples for supervised graph classification. Experimental results show that GraphAug outperforms prior graph augmentation methods on multiple graph classification tasks. The codes of GraphAug are available in DIG [1] library. Fujitsu Research has also been applying graph data augmentation techniques in customer engagements.

Augmentation by Sequential Transformations

We consider graph augmentations as a sequential transformation process. Given a graph $G_0$ sampled from the training dataset, we map it to the augmented graph $G_T$ with a sequence of transformation functions $a_1,a_2,...,a_T$ generated by an automated data augmentation model g. Specifically, at the $t$ -th step ( $t=1,...,T$ ), let the graph obtained from the last step be $G_{t-1}$ , we first use the augmentation model to generate $a_t$ based on $G_{t-1}$ , and map $G_{t-1}$ to $G_t$ with $a_t$ . In our method, $a_1,a_2,...,a_T$ are all selected from three categories of graph transformations:

Node feature masking (MaskNF), which sets some values in node feature vectors to zero
Node dropping (DropNode), which drops certain portion of nodes from the input graph
Edge perturbation (PerturbEdge), which produces the new graph by removing existing edges from the input graph and adding new edges to the input graph.

Our augmentation model g is composed of three parts. They are a GNN based encoder for extracting features from graphs, a gated recurrent unit (GRU) [2] model for generating augmentation categories, and four multi-layer perceptron (MLP) models for computing probabilities. We use a graph isomorphism network (GIN) [3] model as the encoder. At the t-th step, we first add a virtual node into the graph $G_{t-1}$ and add edges connecting the virtual node with all the other nodes. We use the virtual node here to extract graph-level information. The GNN encoder performs multiple message passing operations on $G_{t-1}$ to obtain a node embedding for every node. Then the probability of selecting each augmentation category is computed from the virtual node embedding by the GRU model and an MLP model. We sample the exact augmentation category $c_t$ from the probability distribution, then compute the transformation probabilities for all graph elements and produce the new graph $G_t$ depending on $c_t$ as described below:

If $c_t$ is MaskNF, then an MLP model computes the probability of masking each node feature from the corresponding node embedding, then decides whether to mask or not by sampling from a Bernoulli distribution with the masking probability.
If $c_t$ is DropNode, then an MLP model computes the probability of dropping each node from the corresponding node embedding, then decides whether to drop or not by sampling from a Bernoulli distribution with the dropping probability.
If $c_t$ is PerturbEdge, then an MLP model computes the probability of perturbing each edge from concatenation of two corresponding node embeddings, then decides whether to perturb or not by sampling from a Bernoulli distribution with the perturbing probability.

Label-invariance Optimization with Reinforcement Learning

We cannot directly make the model learn to produce label-invariant augmentations through supervised training because we do not have ground truth labels denoting which graph elements are important and should not be modified. To tackle this issue, we implicitly optimize the model with a reinforcement learning based training method.

We formulate the sequential graph augmentations as a Markov Decision Process (MDP). This is intuitive and reasonable because the Markov property is naturally satisfied: i.e., the output graph at any transformation step is only dependent on the input graph, not on previously performed transformation. Specifically, at the t-th augmentation step, we define $G_{t-1}$ , the graph obtained from the last step, as the current state, and the process of augmenting $G_{t-1}$ to $G_t$ is defined as state transition. The action is defined as the augmentation transformation $a_t$ generated from the model g, which includes the augmentation category $c_t$ and the exact transformations performed on all elements of $G_{t-1}$ .

We use the predicted label-invariance probabilities from a reward generation model s as the feedback reward signal in the above reinforcement learning environment. We use graph matching network [4] as the backbone of the reward generation model s. When the sequential augmentation process starting from the graph $G_0$ ends, s takes $(G_0,G_T)$ as inputs and outputs $s(G_0,G_T)$ , which denotes the probability that the label is invariant after mapping the graph $G_0$ to the graph $G_T$ . We use the logarithm of the predicted label-invariance probability as the return of the sequential augmentation process. Then the augmentation model g is optimized by the REINFORCE algorithm, which updates the model by the policy gradient. Prior to training the augmentation model g, we first train the reward generation model on manually sampled graph pairs from the training dataset. During the training of the augmentation model g, the reward generation model is only used to generate rewards, so its parameters are fixed.

Experimental Results

Experiments on Synthetic Graph Datasets

We first show that GraphAug can indeed produce label-invariant augmentations through experiments on two synthetic graph datasets COLORS and TRIANGLES. We first train the reward generation model until it converges, then train the automated augmentation model. To check whether our augmentation model can learn to produce label-invariant augmentations, at each training iteration, we calculate the label-invariance ratio achieved after augmenting graphs in the validation set.

Figure 1: The changing curves of label-invariance ratios.

The changing curves of label-invariance ratios are visualized in Figure 1. These curves show that as the training proceeds, our model can gradually learn to produce augmentations leading to higher label-invariance ratio. In other words, they demonstrate that our augmentation model can indeed learn to produce label-invariant augmentations after training.

Experiments on Benchmark Graph Datasets

We further demonstrate the advantages of GraphAug over previous graph augmentation methods on six widely used datasets from the TUDataset benchmark, including MUTAG, NCI109, NCI1, PROTEINS, IMDB-BINARY, and COLLAB. We also conduct experiments on the ogbg-molhiv dataset, a large molecular graph dataset from the OGB benchmark. We compare different augmentation methods by their achieved classification performance of a GIN model. The classification performance is evaluated on test accuracy for the six TUDataset datasets and test ROC-AUC for the ogbg-molhiv dataset.

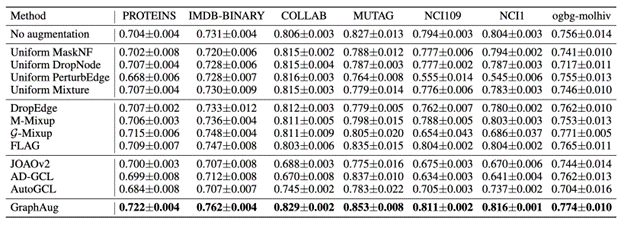
Table 1: The performance of different augmentation methods.

The performance of different methods on all seven datasets with the GIN model is summarized in Table 1. According to the results, GraphAug can achieve the best performance among all graph augmentation methods over seven datasets. Particularly, for molecule datasets including MUTAG, NCI109, NCI1, and ogbg-molhiv, some uniform transformation-based augmentation methods dramatically degrade the classification accuracy. On the other hand, GraphAug consistently outperforms baseline methods, such as mixup methods and existing automated data augmentations in graph self-supervised learning. The success on graph benchmark datasets validates the effectiveness of our proposed GraphAug method.

References

[1] Liu, M., Luo, Y., Wang, L., Xie, Y., Yuan, H., Gui, S., ... & Ji, S. (2021). DIG: A turnkey library for diving into graph deep learning research. The Journal of Machine Learning Research, 22(1), 10873-10881.
[2] Cho, K., Merrienboer, B., Gulcehre, C., Bougares, F., Schwenk, H., & Bengio, Y. (2014). Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation. In EMNLP.
[3] Xu, K., Hu, W., Leskovec, J., & Jegelka, S. How Powerful are Graph Neural Networks?. In International Conference on Learning Representations.
[4] Li, Y., Gu, C., Dullien, T., Vinyals, O., & Kohli, P. (2019, May). Graph matching networks for learning the similarity of graph structured objects. In International conference on machine learning (pp. 3835-3845). PMLR.