
こんにちは.人工知能研究所 自律学習PJの竹森です.富士通研究所では「自律的に学習可能なAI技術」に関する研究開発を行っています.このたび,我々の研究成果である「ロバスト性を考慮したベイズ最適化」に関する研究論文が,機械学習の主要な国際会議であるICML2022に採択されたので,その内容を紹介します.
対象論文
- タイトル:Distributionally-Aware Kernelized Bandit Problems for Risk Aversion
- 発表会議:Thirty-ninth International Conference on Machine Learning (ICML 2022)
- 論文へのリンク
採択された論文の内容
概要
ベイズ最適化
ベイズ最適化とは,評価値を得るのが高コストであるような未知関数を逐次的に評価値を観測しながら,できるだけ少ないサンプル数(評価回数)で最適化を行うことを目的とする問題設定です.材料工学,創薬,機械学習モデルのハイパーパラメータ調整など多くの応用をもつだけでなく,多くの手法は理論的な性能保証が与えられています(例えば,Srinivas et al 2010).
ロバスト性を考慮したベイズ最適化
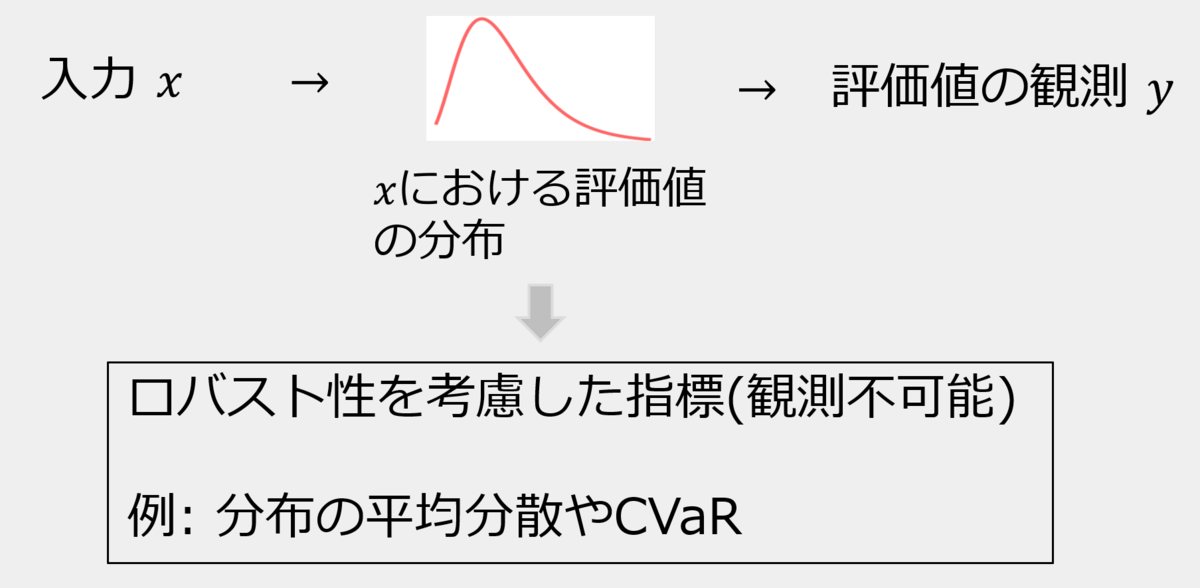
通常のベイズ最適化は,未知関数に対して評価値の平均値が最適化(最大化)されるように探索や観測履歴の活用を行います.しかし,このような最適化を行うと,平均的には良い評価値だが,リスク時(低確率で起きる悪い事象)において評価値が悪くなる可能性があります.例えば,医療診断のために通常のベイズ最適化を適用する際(例えば医療診断AIのためのハイパーパラメータ調整)に,一部の平均的でない患者の集団に対して性能が劣化する可能性があります.このように,一度の意思決定が重要な影響を及ぼす分野においては,平均的な評価値を最適化するより,リスク時の評価値を最適化するほうが適切な場合があります.
今回採択された論文Distributionally-Aware Kernelized Bandit Problems for Risk Aversionでは,ロバスト性を考慮した指標(リスク回避指標) を最適化します.ここで,リスク回避指標として,具体的には平均分散(Mean-Variance)やCVaR(Conditional Value at Risk)を考えています.
論文の貢献
我々の論文では,このようなロバスト性を考慮したベイズ最適化をCVaRやMean-Varianceを最適化するための問題としてとらえ,そのためのモデルの数学的な定式化を与えました.さらに,既存手法の実用上の課題を解決するようなアルゴリズムを複数提案し,それらのいくつかは理論上ほぼ最適であることを証明しました.以下でより詳しく説明します.
既存手法の問題点
CVaRのためのベイズ最適化手法は存在していましたが(Nguen et al, 2021),評価値の分布を考慮にいれるため,実用上制限のあるモデルになっています.(Nguen et al, 2021)での農業での具体例を用いて説明します.ある作物の収穫量を最大化するために,肥料の成分を収穫量を観測しながら逐次的に最適化したいとします.その際に,リスク時(悪天候など低確率で起きる悪い事象)においても収穫量を最大化するために,CVaRのようなロバスト性を考慮した指標を最適化したいとします. (Nguen et al, 2021)のような既存手法がもつ実用上の制約の一つに環境ランダム変数に関するものがあります.環境ランダム変数とは,評価値の観測(農業の例では収穫量)のランダム性の要因となるものであり,農業の例では,降雨量や温度,日射量などを表しています.既存手法はこれらの要因がすべて分かっている場合に適用できますが,収穫量のランダム性の要因となりうるものを全て列挙するのは困難です.さらに,環境ランダム変数の次元が大きいほど最適化の効率が悪化するという問題も抱えています.
分布を考慮したモデルの定式化
ガウス過程や再生核ヒルベルト空間(RKHS)などのモデルは,通常のベイズ最適化で未知関数をモデル化するのに使われています.しかし,CVaRなどのリスク回避指標をモデル化する目的のためには,パラメータ(未知関数の入力)に対して変化する確率分布をモデル化する必要があります.そのためガウス過程やRKHSを使うのは適切でなく,既存研究は無理にこれらを用いてモデル化を試みたので実用上の制約が生じていました. 既存研究の課題を解決するため,我々の論文では,Kernel Mean Embeding (KME)やConditional Mean Embedding (c.f.,Muandet et al, 2017)を用いてモデル化しています.KMEとは,確率分布をRKHSというベクトル空間内のベクトルとして埋めこむ技術です. 我々の論文では,単にモデル化にKMEを使っているわけではなく,ベイズ最適化の問題設定にあったモデルの定式化を与え,そのおかげで,以下の「理論的な結果」で述べるリグレットの下界などの結果が得られました.
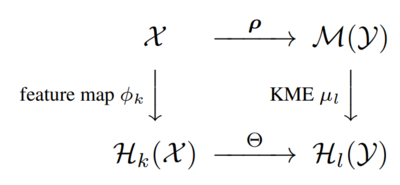
図式(可換図式)はモデルの仮定を表しています.Feature map φによって,入力空間Xをベクトル空間(より正確にはRKHS)H(X)に,KMEによって,評価値の確率測度のなす空間M(Y)をベクトル空間H(Y)に埋めこんでいます.
写像ρは入力に対して変化する評価値の確率分布への対応を表し,Θは対応の滑らかさを定義しています.写像Θはベクトル空間の間の写像となっており,入力空間から確率測度がなす空間への写像であるρより扱いやすい対象になっています.
理論的な結果
上で定式化したモデルを用いて,ベイズ最適化アルゴリズムによって得られた観測履歴(独立同時分布とは限らない)を用いたCVaRやMean-Varianceの推定値を与え,推定の不確実性を評価するconcentration不等式を証明しました.モデルの定式化を与えて,concentraition不等式を証明したのちは,UCB(upper confidence bound)のような標準的なアルゴリズム(Srinivas et al, 2010)と同様のアルゴリズムを考えることができるので,アルゴリズムの詳細は省略します.具体的には以下を証明しました.
- CVaRとMean-Varianceに対しては,UCBタイプのアルゴリズムを考案し,それらの性能保証を与える不等式(累積リグレットの上界)を与えました.
- CVaRに関して,phased elimination(Lattimore et al 2020)に基づくアルゴリズムを考案し,それが性能保証を持つだけでなく,理論的にほぼ最適であることを証明しました.つまり,どんなアルゴリズムも提案手法の性能を本質的に超えることができないことを証明しました.
実験的な結果
CVaR最適化のためのUCBタイプの提案手法(CVPKE-UCB)と既存手法をシミュレータを用いて比較した結果を紹介します.このシミュレータ環境では,環境ランダム変数は未知なのでCVaR最適化のための既存手法(Nguyen et al, 2021)は適用できません.そのため,通常の評価値の平均を最適化するベイズ最適化手法であるIGP-UCBと比較しています.入力に応じて変化する評価値の分布として,提案手法が歪な分布でもうまくいくことを示すため,対数正規分布を考えています(正規分布の場合も実験し,同様の結果を得ていますが,ここでは省略します).
グラフの横軸は,観測した回数を表していて,縦軸はCVaRに関する累積リグレットを表しています.累積リグレットとは最適な指標とアルゴリズムが実際に得た指標との差分の累積和で定義され,小さいほど良い値です.αは評価指標であるCVaRのパラメータであり,リスクレベルと呼ばれる正の数です.αが1のときは,CVaRは平均に一致し,αが小さいときは低確率で起きる悪い事象を考慮した指標になっています.理論的な結果が示唆する通り,提案手法はどの設定でも小さなリグレットを達成しているのに対し,αが小さい場合(CVaRが平均と異なっている場合)は,従来の手法(IGP-UCB)は効率的な最適化に失敗しています.

参考文献
- Lattimore, T., Szepesvari, C., and Weisz, G. Learning with Good Feature Representations in Bandits and in RL with a Generative Model. ICML, 2020.
- Muandet, K., Fukumizu, K., Sriperumbudur, B., and Scholkopf, B, Kernel mean embedding of distributions: A review and beyond, Foundations and Trends in Machine Learning, 2017.
- Nguyen, Q. P., Dai, Z., Low, B. K. H., and Jaillet, P, Optimizing Conditional value-at-risk of black-box function, NeurIPS 2021
- Srinivas, N., Krause, A., Kakade, S., and Seeger, M. W., Gaussian Process Optimization in the Bandit Setting: No Regret and Experimental Design, ICML 2010.
終わりに
富士通研究所では一緒に働ける方やインターンシップを随時募集しています.もし興味を持たれた方がいらっしゃいましたら,自律学習PJの小橋がカジュアル面談を行いますので,是非ご連絡ください.