理論上最高効率の量子ニューラルネットワークを発明！～複雑性の中に潜む美しさ～

こんにちは、量子研究所の鎮西です！私は2025年3月28日に開催されたFujitsu Quantum Day 2025 Japanにおいて、量子ニューラルネットワークの学習効率に関する最新の研究成果について発表を行いました。今回はその内容について解説します。世界最先端の研究動向だけでなく、量子ニューラルネットワークの中に潜む「美しさ」もお伝えできればと思います。

この成果は、量子機械学習分野における世界最大の国際会議Quantum Techniques in Machine Learning 2024で口頭発表にも採択され、世界的にも高く評価していただきました[1]。同じ内容で論文[2]も公開していますので、ご興味がある方はそちらもぜひご覧ください。

量子ニューラルネットワークとは

概要

量子コンピュータは、量子力学の原理を用いることで従来のコンピュータ（以降、古典コンピュータ）では解くことが難しかった様々な問題を高速に解決できると期待されている夢の計算技術です。その応用の一つが、量子計算と機械学習を融合させた量子機械学習になります。機械学習は昨今の大規模言語モデルをはじめとする多くの技術革新のキモとなる技術ですが、量子機械学習はそれに量子計算を組み合わせることで、学習の加速や複雑なデータの処理など、機械学習の可能性をさらに広げることを目指して提案されました。特に、分子や固体など量子力学に従う物質データは古典コンピュータで直接扱うことが難しいため、量子機械学習を活用することで、創薬や材料開発などの分野において大きな進展が期待されています。

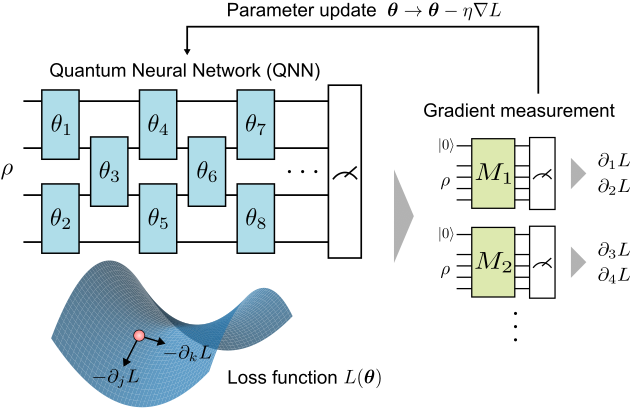
量子ニューラルネットワーク（QNN）は、古典のニューラルネットワークモデルを量子化した量子機械学習の代表的な技術のひとつです。 QNNでは、データを量子コンピュータに入力し、ある量子回路を作用させた後、最後に量子測定を行って出力を得ることで分類や回帰などのタスクを実行します。 QNNの量子回路はパラメーター $\theta=(\theta_1,\theta_2,\cdots)$ で特徴づけられており、問題に合わせて定義された損失関数 $L(\theta)$ をパラメーター最適化によって小さくしていくことでデータを学習していきます。機械学習においては、このパラメーター最適化をいかに効率良く行えるかが、扱える問題の大規模化や精度の向上にとって重要になります。代表的なパラメーター最適化手法として勾配降下法と呼ばれるものがあります（図１）。これは、量子測定によって得られた損失関数の勾配に基づき、パラメーターをそれと逆方向に少しずつ変化させていくことで損失関数を最小化していく手法です。古典のニューラルネットワークと同様に、QNNにおいても勾配降下法は有効であると考えられています。

課題

QNNの課題の一つは、パラメーター最適化時の勾配測定の非効率性です。古典のニューラルネットワークでは、誤差逆伝播法と呼ばれる方法を用いることで、パラメーターの数に拠らず一回の順伝播と一回の逆伝播の計算だけで勾配を計算することができます。この方法は、数千億個のパラメーターを持つと言われている現代の深層学習では必須の技術です。

一方QNNでは、誤差逆伝播法のような効率的かつ汎用的な勾配測定アルゴリズムは未だ提案されていません。最もよく使われている手法としてパラメーターシフト法と呼ばれるものがあります[3]。これはパラメーターの値をひとつずつ $\pm\pi/4$ だけシフトさせながら測定していくことで厳密な勾配が得られる非常に簡便な手法です。しかし、この手法では勾配の各成分を一つずつ測定していく必要があるため、計算コストがパラメーター数に比例し、パラメーターを大量に持つ大規模なQNNに適用するのは困難です。

QNNにおいて効率的な勾配測定が難しいのは、量子力学の制約によるものです。例えば、古典の誤差逆伝播法では、順伝播中の計算結果を逐一コピーし保存していく必要がありますが、量子力学においては量子状態をコピーすることは不可能であることが知られています。これが直接的な原因となって、今までの多くの研究ではパラメーターシフト法などの勾配成分を一つずつ個別に計算していく方法が主に採用されてきました。最近では新たな研究の方向性として、この制約の下で効率的に勾配を計算するアルゴリズムが徐々に模索され始めており[4]、例えば特殊な構造を持ったQNNを使うことによって複数の勾配成分を同時測定する方法が提案されています[5]。しかし、量子力学の原理の下でどの程度まで勾配測定効率を向上させられるかという理論限界はいまだに解明されておらず、効率的な勾配計算アルゴリズムの理論は確立していませんでした。

これらの背景を踏まえて、私たちは二つの研究成果を得ることができました[2]：

量子力学の原理の下で、勾配測定効率の理論限界を解明
勾配測定効率の理論上限を達成する最適なQNNモデルを提案

以下ではこれらの成果についてご紹介していきます。

研究成果

勾配測定効率と表現力のトレードオフ

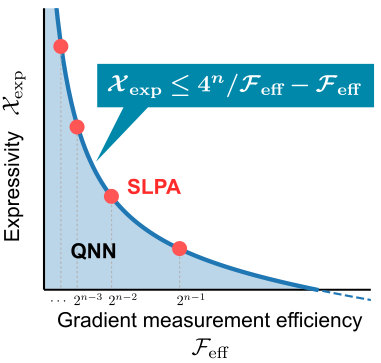
まず一つ目の成果は、QNNにおける勾配測定効率の理論限界を解明したことです。この成果において重要な役割を果たす二つの要素があります。ひとつは先程から話に出ている「勾配測定効率（ $\mathcal{F}_\text{eff}$ ）」と呼んでいるものです。この研究ではQNNの理論限界を探るため、まず勾配測定効率を数学的に厳密な形で定義することから始めました。具体的には、量子力学の原理に従う全ての勾配測定アルゴリズムの中で、同時測定できる勾配成分数の最大値を勾配測定効率と定義します。例えば、パラメーターシフト法などを使ってパラメーター毎に勾配成分を独立に計算していく必要がある場合は、勾配測定効率は１となり、効率の悪いモデルということになります。これが2,3,4,...と増えていくにしたがって同時測定可能な勾配成分数が増えていき、より効率的な勾配計算が可能になります。もうひとつの重要な要素は、QNNの「表現力（ $\mathcal{X}_\text{exp}$ ）」と呼ばれるものです。これはQNNの複雑性を表しており、表現力が高まれば高まるほど、QNNは様々な関数を表現できるようになります。学習するデータや問題が複雑な場合は、この表現力を高めなければ高い精度で学習することが困難になります。

私たちは、「勾配計算効率（ $\mathcal{F}_\text{eff}$ ）」と「表現力（ $\mathcal{X}_\text{exp}$ ）」の間にトレードオフの関係が成り立つことを発見し、数学的に証明しました（ $n$ は量子ビット数）： $$ \mathcal{X}_\text{exp} \leq \frac{4^{n}}{\mathcal{F}_\text{eff}} - \mathcal{F}_\text{eff}. $$ この不等式が意味していることは、勾配を効率的に測定したければモデルの表現力を落とさなければいけないし、逆にモデルの表現力を大きくしたければ勾配測定効率は下げざるを得ない、ということです。つまり、QNNにおける勾配測定効率の原理限界は、実はモデルの表現力で決まってしまうのです。 複雑で多様なQNNが、このような非常にシンプルで美しい不等式に支配されていることは驚くべき事実だと思います。 この結果は、QNNの限界と可能性を明らかにすると共に、効率的なQNN設計の指針を与えるものになりました。

理論上最高効率のQNNを提案

勾配測定効率の上限の存在が明らかになった一方、QNNには量子重ね合わせの効果によって古典機械学習の性能を凌駕する可能性が秘められています。その可能性を最大限引き出すための次なる目標は、勾配測定効率の原理限界を達成する、すなわち理論上最も効率的に勾配計算が可能なQNNモデルを見つけることです。私たちは実際に、Stabilizer-Logical Product Ansatz (SLPA)という新しいQNNモデルを提案し、それがある表現力の下で勾配測定効率の上限を達成する最適なモデルであることを示しました。 SLPAは、複数のブロックから構成されており、それぞれのブロックにはいくつかの回転ゲートが含まれています。このモデルでは、ある特別な方法で量子回路を構成することによって、ブロック内の勾配成分を全て同時に計算することが可能になります。これは、パラメーター毎に勾配成分を計算する必要のあった従来のQNNモデルとは対照的に、非常に効率的な勾配計算が可能であることを意味しています。

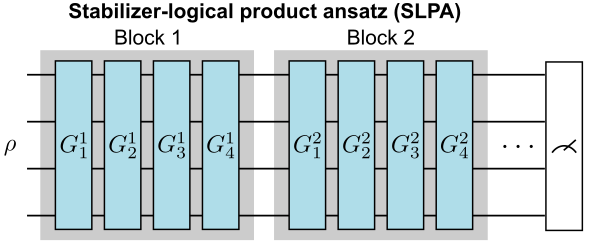
図３：SLPAの概要図。 $G^{a}_{j}$ は $a$ 番目のブロックの $j$ 番目の回転ゲートの生成子を表す。

図３：SLPAの概要図。 $G^{a}_{j}$ は $a$ 番目のブロックの $j$ 番目の回転ゲートの生成子を表す。

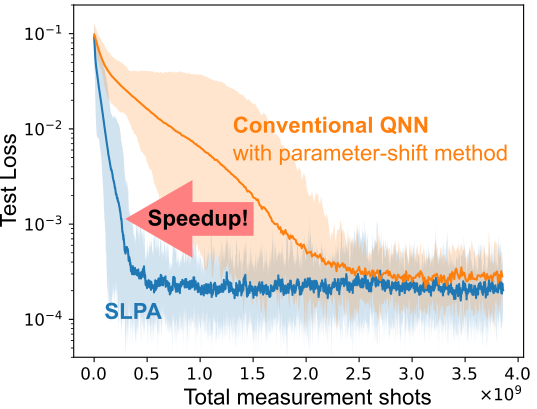
SLPAはその特殊な構造から、対称性が絡んだ問題に対して特に強力な性能を発揮します。私たちは、SLPAの有効性を、ある対称性を持つ未知の関数を学習するという問題で実証しました。これは幾何学的深層学習[6, 7]と呼ばれる分野での標準的な問題設定であり、分子動力学、電子状態計算、コンピュータビジョンなど様々な応用が考えられています。下の図は学習プロセスにおける損失関数の変化を表しており、この値の減少が早ければ早いほど、そのモデルはより効率的であるということになります。図が示す通り、パラメーターシフト法に基づく従来のQNN（オレンジ）と比較して、私たちの提案モデル（青）は劇的に学習時の計算回数を減らすことに成功しました。この結果は、理論上の最適性に加えて、実際の問題における提案モデルの高い効率性を示すものになっています。

おわりに

今回の研究では、QNNの勾配測定効率に関する基礎理論を確立し、そのポテンシャルを最大限引き出すための設計指針を与えることができました。複雑なQNNの中に、あれほどシンプルで美しい不等式が潜んでいることを発見したときは、自分自身とても感動したことを覚えています。一方、QNNの実用化にはまだまだ多くの課題が残されています。それらを解決するためには、既存研究を発展させるだけでなく、従来の枠組みを超えた真に新しい量子機械学習アルゴリズムの登場が必要かもしれません。私自身も、量子AIの実現を目指して、多角的な視点から研究を続けていきたいと思います。

最後までご覧いただき、ありがとうございました！