量子コンピュータを活用した材料物性シミュレーション技術の開発#1：量子コンパイル技術 - fltech

こんにちは、量子研究所で量子アルゴリズムの研究をしております松本徳文です。先日2025年3月28日にUvance Kawasaki Towerにて富士通主催のグローバル量子コンピューティングイベント「Fujitsu Quantum Day」が開催されました。その中で私たちの研究チームの最近の成果をポスター発表しましたので、その内容をご紹介したいと思います。

ポスター発表内容の概要

私たちの研究チームでは、2022年度より量子コンピュータ向けソフトウェア開発に強みを持つスタートアップの株式会社QunaSysと連携して、実社会問題への応用を目指した量子アルゴリズムの研究開発に取り組んでいます。特に本共同研究では、量子コンピュータによる計算高速化が有力視されている材料科学分野（電池、触媒、新素材、創薬など）の問題をターゲットとし、近い将来に実現される Noisy Intermediate-Scale Quantum (NISQ)~early Fault-Tolerant Quantum Computing (FTQC)デバイスの使用を想定した革新的アルゴリズムの提案を目指しています。今回のポスターセッションでは、2023年度の研究成果である量子コンパイル技術（Local Subspace Variational Quantum Compilation, LSVQC）[1]と有限温度シミュレーション技術（Markov-Chain Monte Carlo with Sampled Pairs of Unitaries, MCMC-SPU）[2]について発表しましたので、本稿と次稿に分けて内容をご紹介します。以下では、１点目の量子コンパイル技術について簡単に解説します。

量子コンパイル技術

背景

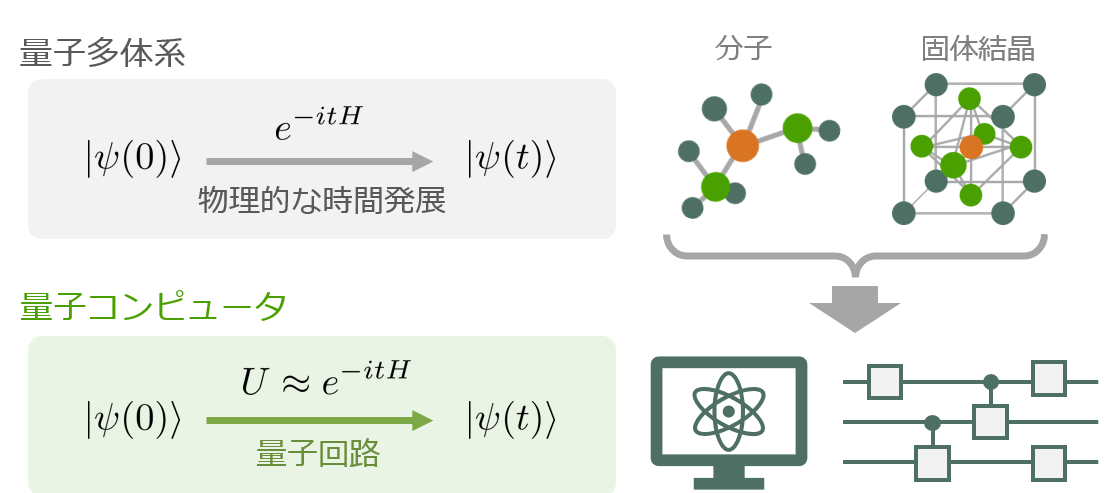
量子多体系のシミュレーションは指数的な量子加速が期待される実用的な問題の１つです。具体的には分子や固体結晶といった量子多体系の時間発展をシュレーディンガー方程式に基づいて解析することで、物性物理や量子化学の問題を解くことができます。これを量子コンピュータ上では、時間発展演算子を近似する量子回路を使って再現します（図１）。つまり、この問題では時間発展演算子をいかに効率的かつ高精度に量子回路として実装できるかが重要です。

これまで、様々な時間発展演算子の実装手法が提案されていますが、特に代表的なものがTrotter分解です。Trotter分解はシンプルな回路構造で実装が簡単ですが、精度を上げるためには深い回路が必要になり、計算時間の増加やデコヒーレンス、エラーの蓄積といった問題が生じます。その他、NISQ向けの変分手法は現在の実機でも実装が可能ですが、実応用で有用な大規模問題へのスケールアップは困難です。このようなことから、特にNISQ～early-FTQC時代の近い将来での実用化を見据えると、少ない計算リソースでかつ大規模化可能な時間発展演算子の実装手法が望まれます。

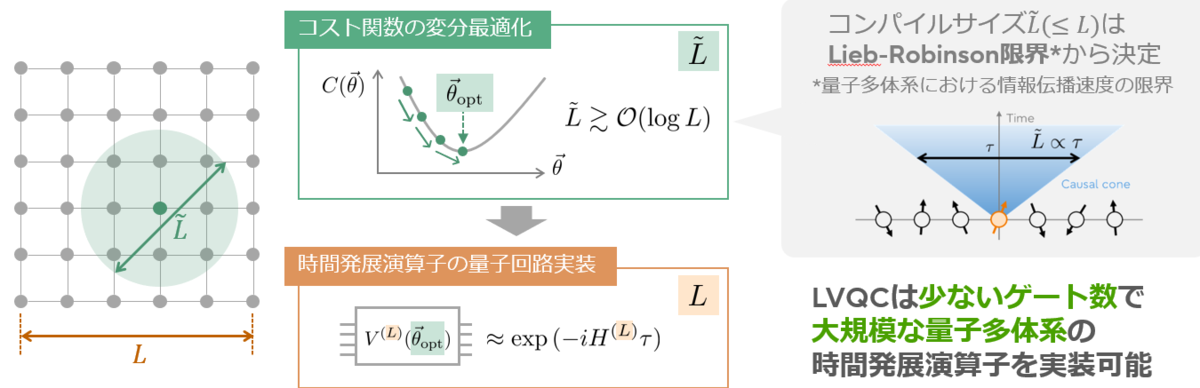
そこで近年提案されたのがLocal Variational Quantum Compilation (LVQC) [3][4]という手法です（図２）。LVQCでは、まず大規模量子多体系から小さな部分系を取り出し、この部分系上で近似誤差（コスト関数）を最小化する回路パラメータθoptを求めます。そして、それらを使って、元の大規模系の時間発展演算子を量子回路に実装します。この手法は「Lieb-Robinson限界」という、量子多体系における情報伝播速度の限界に基づいています。このLVQCを使えば、少ないゲート数で大規模な多体系の時間発展演算子を実装することが可能となります。

一方、LVQCにも課題があります。それは部分系のサイズが大きいとコスト関数測定が困難になる点です。LVQCではターゲットである厳密な時間発展演算子に対する状態空間全体における平均誤差を最小化します。この量は部分系のサイズの2倍の量子ビットと、離れた量子ビット間のエンタングルゲートを使って測定するため、サイズが大きいと量子実機での実装が難しくなります。また関連して、LVQCでは計算したい物理量の誤差を直接最小化するわけではないため、実際のダイナミクス計算では十分なリソース削減ができない場合があります。

これらの課題に対し、実際の応用では状態空間全体ではなく特定の部分空間での時間発展を再現できればよいケースがほとんどである、ということに私たちは新たに着目しました。例えば、物性や量子化学の問題では、低エネルギー領域や結晶のような特定の対称性を反映した部分空間でのダイナミクスのみが重要です。そこで、特定の部分空間に限定して最適化すれば、実際の物理量計算において、さらなるリソース削減と高精度化が可能なのではないかと考えました。

新手法の提案

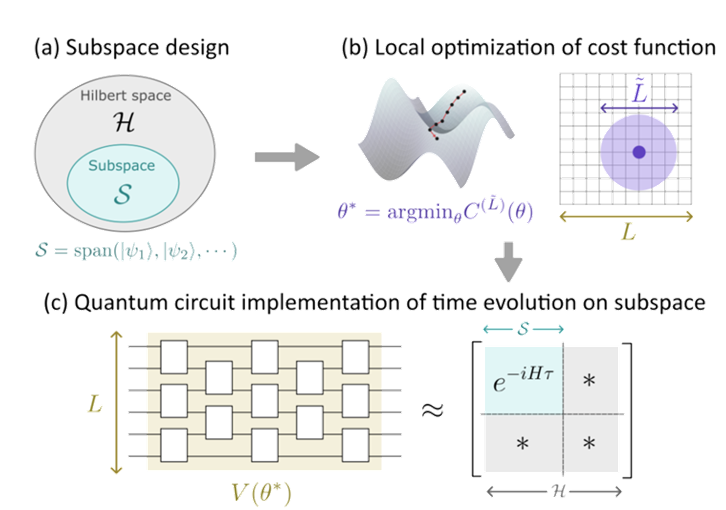
このような背景のもと、私たちはLocal Subspace Variational Quantum Compilation (LSVQC) という新手法を提案しました。 LSVQCは小さな部分系における最適化計算を通じて、大規模な多体系の“特定の部分空間における”時間発展を実装する手法です。具体的には図３のように、部分空間のデザイン、ローカルなコスト関数の最適化、大規模時間発展演算子の実装、という流れで実行されます。特にLVQCと違い、解きたい問題の性質に応じてまず部分空間を設計し、その部分空間上でのみ時間発展の再現を行うのがポイントです。 LVQCと性能比較をすると、まず量子実機でのコスト関数測定が容易で、さらに実際の物理量をより効率的かつ高精度に計算可能というメリットがあります。

数値検証

次に、量子回路シミュレータを用いた数値計算により、LSVQCの性能を評価しました。特に実際の材料解析への応用を想定して、Sr₂CuO₃という強相関の反強磁性物質に対する計算を行いました。具体的には、第一原理バンド計算の結果から有効的なHubbard模型を構成し、LSVQCを用いて線形応答などの解析で重要なGreen関数を計算しました。

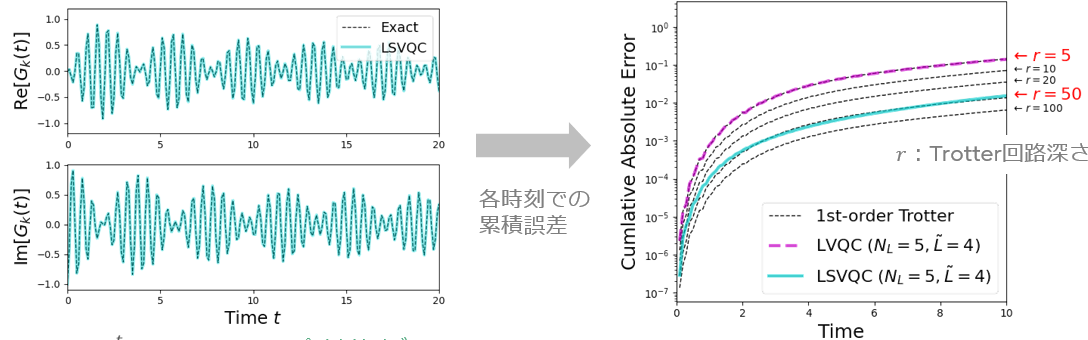
計算結果が図４です。LSVQC（緑実線）は厳密なダイナミクス（黒点線）と重なっており、精度良く再現していることが分かります。また、誤差を見ると、回路深さ5に相当するLVQCは回路深さ5のTrotter分解と重なっており、リソース削減できていません。これに対し、同じく回路深さ5に相当するLSVQCは回路深さ50のTrotter分解と重なっており、回路深さをTrotter分解に比べて約1/10に削減できることが分かりました。このように、Green関数のような複雑なダイナミクスでも、安定してリソース削減できることがLSVQCのメリットです。

まとめ

本研究では小さな部分系での最適化計算を通じて、大規模量子多体系の特定の部分空間における時間発展を効率的に実装する新手法「LSVQC」を提案しました。既存手法のLVQCに比べてコスト関数測定にかかるリソースが削減され、さらに物理量計算における精度とリソース削減率が向上します。実際の強相関物質を模擬した模型に対する数値シミュレーションを行い、Trotter分解とLVQCに対する優位性を実証することができました。今後の展望としては、NISQやearly-FTQCにおけるリソース見積もりや、他のモデル・物理量に対する検証、実機実験などを考えています。

次稿の「量子コンピュータを活用した材料物性シミュレーション技術の開発#2：有限温度シミュレーション技術」[5]では、ポスター発表内容の２点目である有限温度シミュレーション技術（MCMC-SPU）についてご紹介する予定です。ご期待ください！