Hello, I am Omar Ragheb from Computing Laboratory. Fujitsu have been developing reconfigurable architectures and CAD tools to accelerate AI workloads. In June 2024, we presented a mapping algorithm at the flagship DAC conference in the field of design automation.
This achievement has been done with the collaboration with the University of Toronto.
Paper Information
Title: CLUMAP: Clustered Mapper for CGRAs with Predication
Venue: Design Automation Conference DAC ’24, June 23–27, 2024, San Francisco, CA, USA
Authors: Omar Ragheb, Jason Anderson
Contributions
We present an architecture-agnostic CGRA mapper that supports multi-context, and predication architecture features, offering flexibility to target various architectures. The mapper extends prior work done by Ragheb et al. [1], incorporating two enhancements to accelerate the placement and routing processes within mapping. The first addition is clustering, which is used as a preprocessing step before placement and routing. Clustering, hence “CLUMAP”, ensures that interconnected operations are placed together, leading to a more compact placement. This allows simulated annealing to find solutions that utilize fewer CGRA PEs, freeing up more resources throughout the CGRA to be utilized. The clustering step eases the mapping process for intricate PE architectures, particularly those containing PEs that support predication. The second enhancement introduces a new cost function for simulated annealing placement that accounts for the operation scheduling. The cost function improves the utilization of the CGRA interconnect, leading to more efficient routing by balancing interconnect demand across contexts.
Technology
Clustering
CGRA architectures have experienced an increase in complexity to support a broader range of applications, incorporating intricate features such as predication networks, the integration of multiple ALUs within a single PE, and the introduction of heterogeneous PEs. Additionally, routing within a PE maybe constrained causing the mapping process to be more challenging. To address this, we developed and implemented a clustering algorithm, allowing the grouping of operations within a single PE. The primitives within a cluster are then moved as a unit during placement. Moreover, during the placement phase, which utilizes the simulated annealing algorithm, clusters have the capability to be placed together on the same PE if they use different functional primitives within a PE. The clustering algorithm begins by traversing the device-model graph, generating PE templates for each distinct PE structure. Its primary objective is to accommodate as many DFG operational nodes as possible within a PE template, while ensuring the routability of dataflow edges Evaluation
Scheduling-Aware Cost function
The placement algorithm presented in the mapping algorithm detailed in [1] utilizes simulated annealing and the common half-perimeter bounding-box wirelength (HPWL) cost function. However, this cost function is designed for FPGA architectures, which are significantly different CGRAs in terms of granularity and routing resources. Here, we propose an extended cost function that is aware of the scheduling of operations. The extended schedule-aware cost function (SC) function is utilized in conjunction with the HPWL cost function, as shown in Equation 1
𝑇𝑜𝑡𝑎𝑙𝐶𝑜𝑠𝑡 = 𝛼 ∗ 𝐻𝑃𝑊 𝐿 + (1 − 𝛼) ∗ 𝑆𝐶 (1)
Here, 𝛼 represents a weight parameter, used to flexibly balance the total cost between the HPWL and SC.
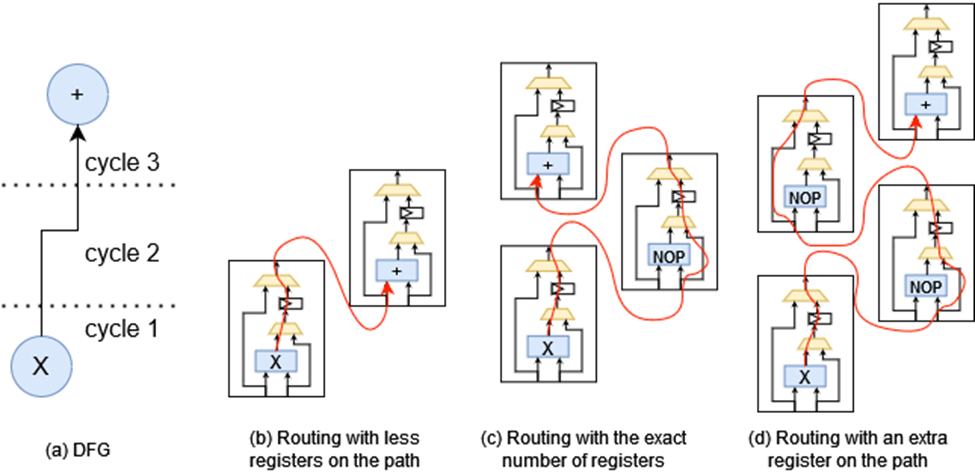
The motivation behind the cost function can be seen in Fig. 1. Given a multiply and add operation, scheduled two cycles apart as shown in Fig. 1a, the ideal placement of the two operations would be two PEs apart as shown in Fig. 1c. However, if the placements of the operations are one PE apart, as illustrated in Fig. 1b, then the routing will struggle to find a correct solution. On the other hand, if the operations are placed more than two PEs apart as shown in Fig. 1d, although the routing would be valid, each extra PE would be used as a bypass, thereby wasting the PE and rendering it unusable for useful computational work. The SC cost function employed to overcome these drawbacks is a scheduling-aware cost function:
𝑆𝐶 = 𝐸𝑒𝑑𝑔𝑒𝑠∑︁(|𝑀𝑑 − 𝐶 |) ∗ 𝐶 (2)
In equation 2, 𝐶 denotes the number of cycles required between these two operations, and 𝑀𝑑 denotes the Manhattan distance between the two placed operations in terms of height, width, and depth (i.e. context index difference). The absolute value of the difference between 𝑀𝑑 and 𝐶, is taken ensuring that the cost is zero if the operations are placed at the optimal distance and non-zero otherwise. Additionally, the cost is scaled by the number of cycles 𝐶, aiming to prioritize edges with more cycles at the ideal distance. Lastly, equation 2 sums up the scaled version of the distance difference between 𝑀𝑑 and 𝐶 for each application dataflow graph edge.
Predication
Predication involves associating data or an operation with a predicate (true/false value) to manage its execution. Consider for example, an if-then-else (ITE) structure, where the "if" statement’s operations are chosen to be executed when the predicate is true. Conversely, operations linked to the "else" statements are chosen to be carried out if the condition is false (i.e. the predicate is false). ITE statements are commonly used in applications, which makes them a barrier to the broadening the applications that can be mapped onto CGRAs. ITE statements can be realized through predication techniques in both hardware and software, making predication a crucial component that CGRAs require to execute applications that contain control flow.
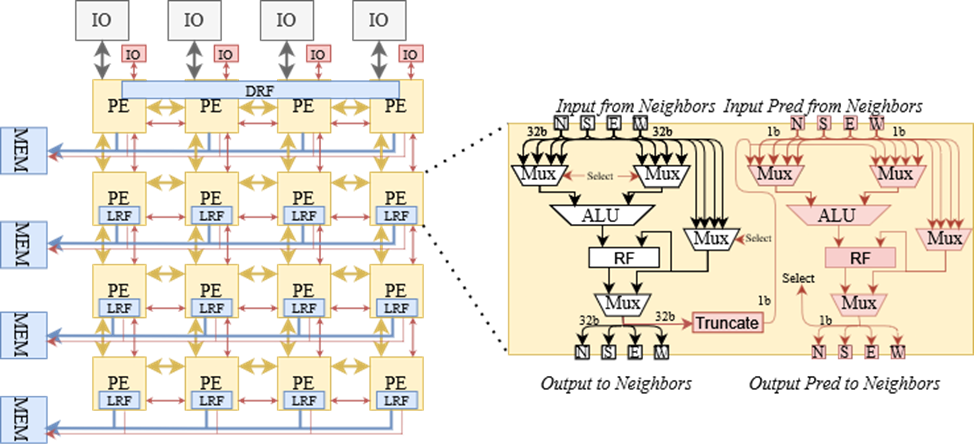
The predication scheme we choose to support is known as partial predication, in which predicates are applied to a partial set of operations that decide the correct result of the application. The support of partial predication entails the following modifications:
- Hyperblock generation: Utilizing an intermediate language such as LLVM or MLIR for the generation of hyperblocks, similar to Liolli et al. [2].
- Architecture extension: Extending the architecture to include a separate 1-bit wide interconnect network, highlighted in red in Figure 2.
- 1-bit ALU Addition: Adding a 1-bit ALU, as shown in Fig. 2,capable of performing bitwise AND, OR, and XOR operations, which are used to merge predicates.
- Multiplexer modification: Modifying multiplexers to implement the SELECT and PHI instructions. This involves loading two configurations into the multiplexer, with the predicate determining which configuration to utilize. When the multiplexer implements neither a PHI nor a SELECT operation, both configurations are loaded with the same value, causing the predicate to be ignored.
- Mapping support: Incorporating mapping support for predicated SELECT/PHI instructions, along with multi-bitwidth interconnect.
All the changes have been implemented within the CGRA-ME tool for both the ADRES and HyCUBE architectures. These adaptations enable the tool to effectively handle partial predication.
Evaluation
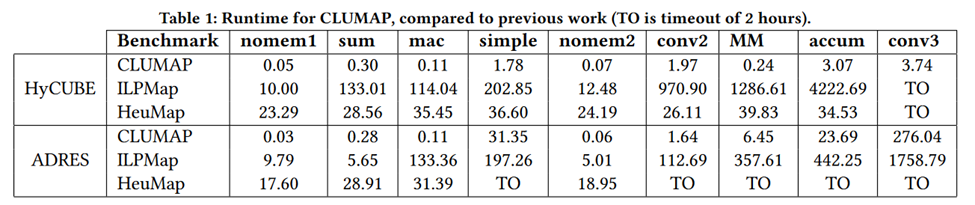
Comparison with previous mappers
We compared this work to earlier mappers within CGRA-ME in terms of runtime. We used the ILP-based mapper (ILPMap) from [3] and heuristic based mapper (HeuMap) presented in [4]. Benchmarks with various DFG sizes are mapped to a CGRA size of 6 × 6 for both HyCUBE and ADRES architectures. Note that the experiments are conducted on DFGs without PHI or SELECT instructions. Any PHI operation present within the DFGs are replaced with back-edges into the operation that feeds the PHI. Additionally, the architectures do not include the predicated architecture changes mentioned in Section 6. This is because previous mappers do not support predicated architectures. The results obtained are summarized in Table 1. As the results show, this work brings about multiple orders of magnitude speedup over previous mappers for all benchmarks. Furthermore, both the ILP-Mapper and heuristic mapper times out (TO) (TO means that the mapper failed to find a valid mapping within a 2-hour time limit) for the conv3 mapping to the HyCUBE architecture. For the ADRES architecture, the heuristic mapper TOs on 5 benchmarks, while ILP and CLUMAP successfully map all benchmarks. CLUMAP demonstrates improved runtime compared to the existing mappers in CGRA-ME. Note also that previous mappers do not guarantee a latency-balanced mapping, while CLUMAP does guarantee it.
Optimization Study
To assess the impact of the optimizations, we mapped a set of 14 benchmarks on predicated HyCUBE architecture. This set comprises the 9 benchmarks used in the previous study, now with predicated PHI instructions to observe the impact on mapping time, and an additional 5 benchmarks that include predication. For the mapping, we employed two mapping strategies:
- Baseline with no optimizations, presented in by Ragheb et al. [1].
- Baseline with clustering and scheduling-aware cost function discussed
The mapping strategies are applied on 6 × 6 single-context and 4 × 4 multi-context HyCUBE architecture.
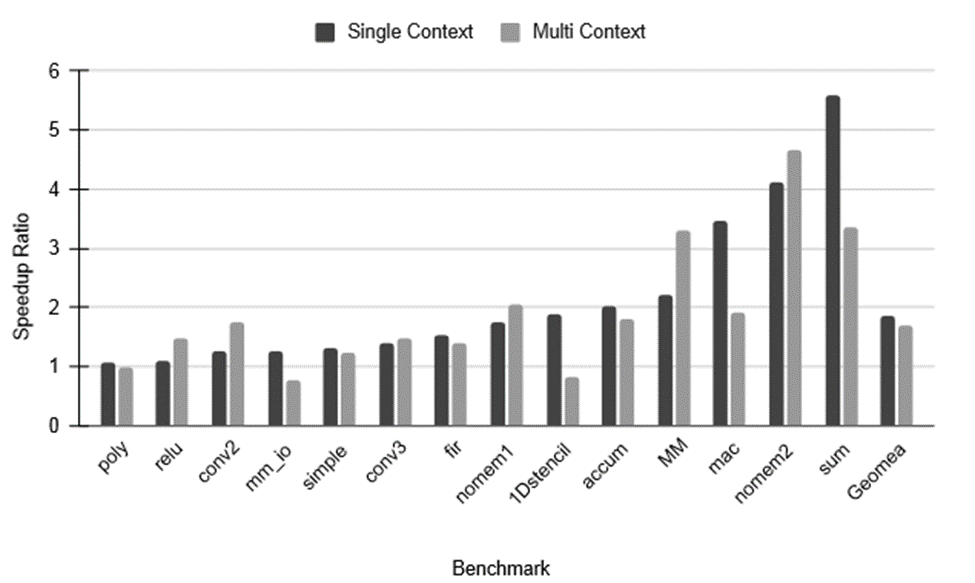
Fig. 3 shows the speedup ratio between the first and third mapping strategies. The dark grey bars represent the mapping of benchmarks on single context, while the light grey bars depict the mapping on a 4 × 4 CGRA with a minimum of 2 contexts. For the single context, the optimization consistently leads to a speedup across all benchmarks, resulting in a geometric mean speedup of 1.89. In the multi-context mapping, there is a degradation for 2 benchmarks, namely mm_io and 1DStencil. However, the other 12 benchmarks experience significant speedups, resulting in a geometric mean speedup of 1.69.
Presentation at DAC
The Design Automation Conference (DAC) is renowned as one of the most competitive and prestigious conferences in the design automation field. In 2024, DAC received over 1000 paper submissions, with a highly selective acceptance rate of only 23%. This year's event took place at Moscone West in San Francisco from June 22nd to 26th.
Attending DAC Conference
Attending DAC 2024 was a great experience, particularly in the exhibition hall where I had the chance to interact with industry leaders like Siemens, Cadence, and Synopsys. Each booth showcased innovative technologies and solutions that are shaping the future of electronic design automation. The level of advancement and creativity on display was truly inspiring, offering valuable insights into the latest trends and developments in the field. Beyond the exhibition, the technical presentations on accelerator architectures were a major highlight. I focused on sessions about accelerators for machine learning (ML) workloads, which provided a deep dive into their impact on performance and efficiency. The evaluations discussed revealed how these accelerators significantly enhance processing power and speed up workloads, underscoring their growing importance in optimizing ML workflows. Overall, DAC 2024 delivered a compelling mix of hands-on exploration and advanced knowledge. The engaging interactions with industry leaders and the in-depth presentations on accelerator architectures offered a comprehensive view of the current landscape and future directions in electronic design automation. The conference was both educational and inspiring, leaving me excited about the innovations on the horizon.
References
- O. Ragheb, R. Beidas and J. Anderson, "Statically Scheduled vs. Elastic CGRA Architectures: Impact on Mapping Feasibility," 2023 IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW), St. Petersburg, FL, USA, 2023, pp. 468-475, doi: 10.1109/IPDPSW59300.2023.00079.
- A. Liolli, O. Ragheb and J. Anderson, "Profiling-Based Control-Flow Reduction in High-Level Synthesis," 2021 International Conference on Field-Programmable Technology (ICFPT), Auckland, New Zealand, 2021, pp. 1-6, doi: 10.1109/ICFPT52863.2021.9609816.
- S. Alexander Chin and Jason H. Anderson. 2018. An architecture-agnostic integer linear programming approach to CGRA mapping. In Proceedings of the 55th Annual Design Automation Conference (DAC '18). Association for Computing Machinery, New York, NY, USA, Article 128, 1–6. https://doi.org/10.1145/3195970.3195986
- M. J. P. Walker and J. H. Anderson, "Generic Connectivity-Based CGRA Mapping via Integer Linear Programming," 2019 IEEE 27th Annual International Symposium on Field-Programmable Custom Computing Machines (FCCM), San Diego, CA, USA, 2019, pp. 65-73, doi: 10.1109/FCCM.2019.00019.
