量子コンピュータの計算効率を劇的改善！STARアーキテクチャの進化と応用

こんにちは、量子研究所の兎子尾です。今回は、私たちが開発を進めている量子コンピュータのソフトウェア技術に関する話題をお届けします。量子コンピュータは未来のテクノロジーとして期待を寄せられており、ここ数年で開発競争が激化しています。その中でも、富士通と大阪大学*1が開発した、量子コンピュータの実用化を早める革新的な技術である「Space-Time efficient Analog Rotation quantum computing（STAR）アーキテクチャ」*2は、過去2回のプレスリリース*3 *4により、世界中の注目を集めつつあります。このSTARアーキテクチャに関して、2025年3月28日に開催されたFujitsu Quantum Day*5にて発表を行いましたので、その内容を解説させていただきます。

量子コンピュータの現状と課題
富士通と大阪大学が開発したSTARアーキテクチャ：量子コンピュータ早期実用化に向けて
STARアーキテクチャの技術的詳細：状態準備プロトコル
STARアーキテクチャのメリット：材料シミュレーションへの応用
まとめ
参考資料

量子コンピュータの現状と課題

現在、量子コンピュータは発展途上にあり、実用的な問題で現行コンピュータの速度を上回る段階にはまだ至っていません。現在主流の量子コンピュータは、Noisy Intermediate-Scale Quantum (NISQ) コンピュータと呼ばれ、ノイズの影響を受けやすく、量子ビット（量子コンピュータの計算単位）の数も限られています。一方、将来的に期待されるのは、Fault-Tolerant Quantum Computer (FTQC) と呼ばれる、ノイズに強く、大規模な量子コンピュータです。

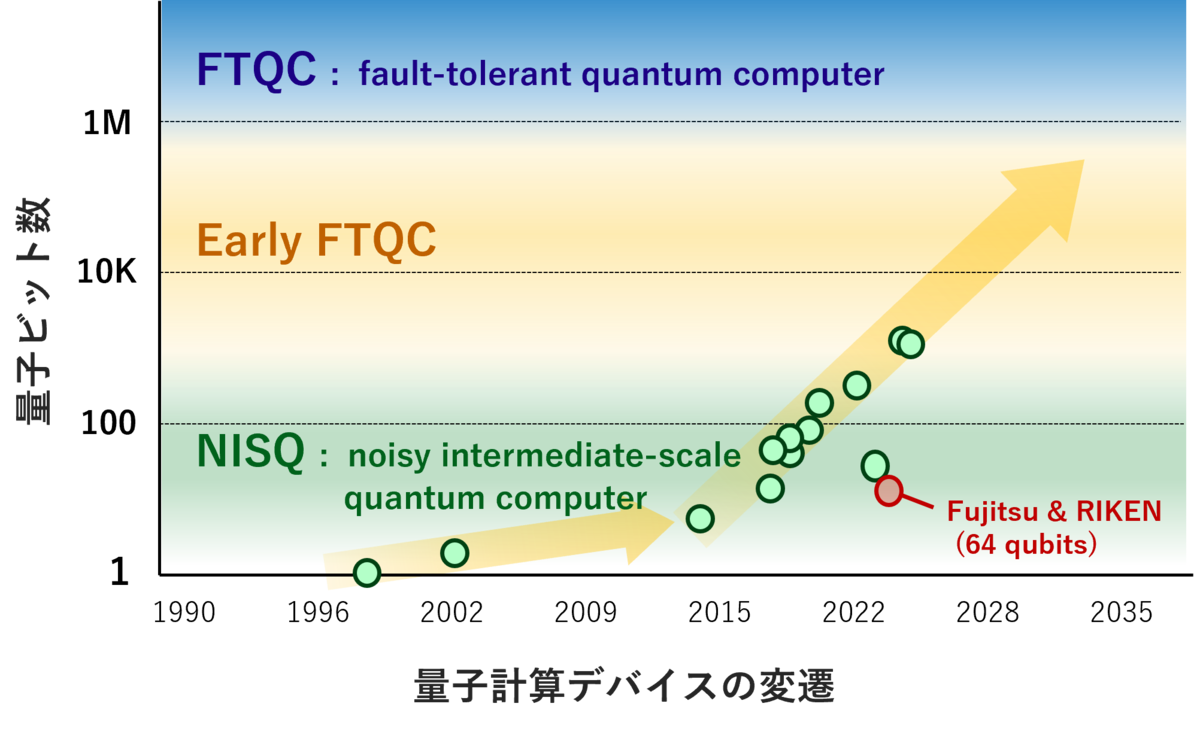
FTQCを実現するためには、以下の2つの課題を克服する必要があります。

大規模化：量子ビットの数を増やす必要があります。
ノイズ対策：量子ビットは非常にデリケートで、熱や電磁気などのノイズの影響を受けやすく、エラーが発生しやすいという性質があります。量子エラー訂正などの技術が必要となります。

量子エラー訂正とは、物理的な量子ビットをいくつも集めてきて、たとえエラーが起こっても検知と訂正を行うことで正しい状態に戻す操作のことです。物理量子ビットの集合を１つのノイズに強い量子ビット（論理量子ビット）とみなし、論理量子ビットを基本単位とすることで、誤り耐性のある計算が可能になります。

ところが大規模化がボトルネックのため、FTQCの到来はまだまだ先と見られており、それまでの黎明期であるEarly-FTQC時代に量子コンピュータを実用化するには、大きなブレイクスルーが必要と考えられています。

富士通と大阪大学が開発したSTARアーキテクチャ：量子コンピュータ早期実用化に向けて

今回ご紹介するSTARアーキテクチャは、量子コンピュータの早期実用化を目指した新しいアプローチです。このアーキテクチャのポイントは、以下の2点です。

位相回転ゲートの直接実装：

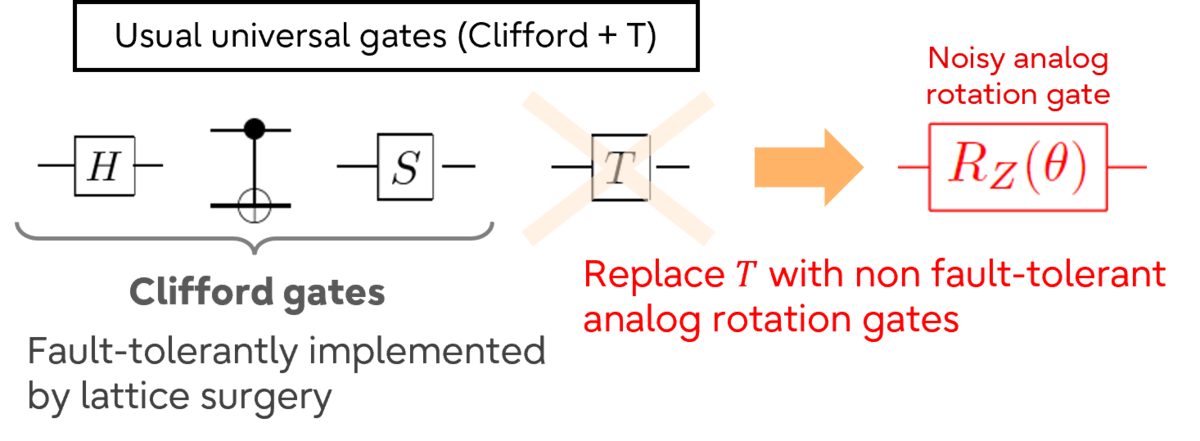
量子計算に必須となる「位相回転」（量子ビットのZ軸周りの回転）という操作を、直接実装できる新しい手法「位相回転ゲート ${\small R_Z(θ)}$ 」（ $θ$ は回転角度）を導入しています。従来の量子計算では、量子ビットの基本操作（現行コンピュータのNOTゲートなどに対応）として、図3で示されるCliffordゲートとTゲートが用いられてきましたが、Tゲートの実装には大きなコストがかかります。STARアーキテクチャでは、位相回転ゲートを用いることで、より効率的な量子計算を実現しようとしています。

部分的な誤り耐性：

位相回転ゲートの弱点として、エラーを完全に防ぐことができません。そのため、独自のエラー検知方法を実行して、防ぎきれないエラーを最小限に抑えることで、比較的高い精度を実現しています。

STARアーキテクチャの技術的詳細：状態準備プロトコル

STARアーキテクチャにおいて重要なのは、位相回転ゲートに必要な初期状態 $|m_θ\rangle_L$ をできるだけ正確に準備するプロトコルです。というのも、位相回転ゲートは計算中の量子ビットに直接操作することはできず、図4のように別に初期状態を準備しておき、その状態を回転させたい量子ビットに転送させるという方法を取ります。

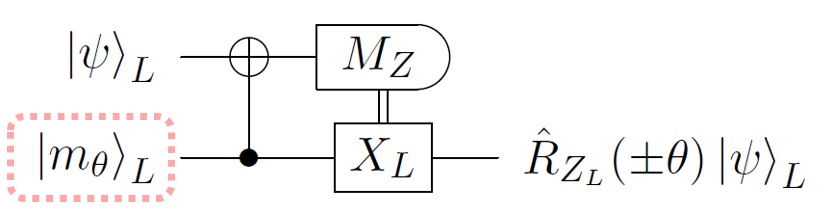
ここで、 $|\psi\rangle_L$ , $M_Z$ , $X_L$ , $R_{Z_L}(θ)$ はそれぞれ回転させたい量子ビットの状態、測定操作、論理量子ビットに対するパウリX演算子、位相回転ゲートを表します。また、初期状態 $|m_θ\rangle_L$ は、以下の式で定義されます。

$|m_θ⟩_L ≡ R_{Z_L} (θ) |+⟩_L=\cos(θ)|+⟩_L+i \sin(θ) |-⟩_L$

STARアーキテクチャでは、これまで位相回転ゲートのエラー率 ${\small P_L}$ は、物理量子ビット１つに対するエラー率を $p$ とすると、 ${\small P_L}= \frac{2}{15}p$ という依存性を持っていました。つまり、 $p ={\small 10^{-3}}$ であれば、 ${\small P_L}$ は $\frac{2}{15}\times{\small 10^{-3}}$ という値になります。

逆に言えば、物理量子ビットのエラー率をこれ以上低くできなければ、位相回転ゲートのエラー率をさらに下げることはできません。物性計算や量子化学計算などの有用な計算ではさらに何桁も低く抑える必要があるため、このままではSTARアーキテクチャをそれらの領域で実用化することは難しい状況でした。

今回、私たちは新しい状態準備プロトコル「Transversal multi-Pauli rotation」*6を開発しました。

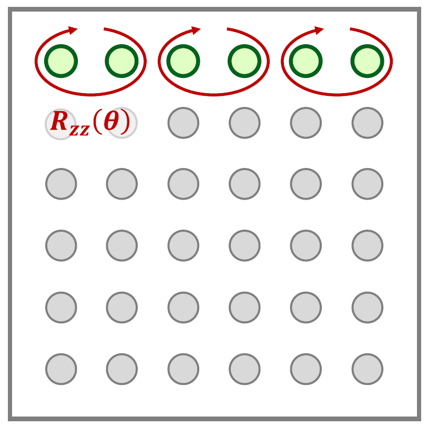
簡単な例として図5のような状況を考えてみましょう。この場合、以下の関係式を利用して初期状態 $|m_θ\rangle_L$ を準備します。

$\begin{aligned} R_{ZZ}(θ) |+⟩_L &= (\cos^3θ\cdot I_L - i \sin^3θ \cdot Z_L) |+⟩_L + \rm{(Pauli\:error\:term)} \\ &∝ R_{Z_L}(θ^*) |+⟩_L + \rm{(Pauli\:error\:term)} \end{aligned}$

ここで、 ${\small R_{ZZ}(θ)}$ は、隣接する量子ビットを2つ同時に Z回転させる操作で、 $Z_L$ は図5の論理量子ビットに対するパウリZ演算子、(Pauli error term) は有効的なエラー項を表し、論理レベルの回転角は $θ^\ast \sim -θ^{3}$ のように与えられます。

この方法では、位相回転ゲートのエラー率は、 $P_L=\alpha θ^\ast p$ で表されます（ $\alpha \sim 1.5$ ）。この関係式の重要なところは、回転角 $θ^\ast$ が小さければ小さいほど、位相回転ゲートのエラー率が下がるということです。これを利用することで、小さい回転角 $θ^\ast$ に対して、STARアーキテクチャの精度を劇的に改善することができます。

STARアーキテクチャのメリット：材料シミュレーションへの応用

新しい状態準備プロトコルの発明によって、STARアーキテクチャは従来よりも複雑なアプリケーションを実行することが可能になりました。以下では、有望な応用例として、材料開発に役立つ2種類のアプリケーションを紹介します（詳細は原論文*6をご参照ください）。

量子ダイナミクスのシミュレーション：

量子コンピュータを使って、物質のミクロな振る舞いをシミュレーションすることができます。例えば、ハイゼンベルクモデル*7などの量子スピン系の時間発展をシミュレーションすることで、磁性材料の動的な挙動を解析したり、新しいスピントロニクスデバイスを設計したりすることが可能になります。

このような解析は現行のコンピュータでもある程度実行できますが、対象とする量子系のサイズが大きくなるにつれて、必要になる計算時間・メモリが指数的に増加してしまうことが広く知られています。他方、STARアーキテクチャを用いれば、古典では扱えない規模の量子系を多項式時間でシミュレートできると期待されます。本研究では簡単な具体例として、ランダム磁場下の1次元ハイゼンベルクモデル（図6）のダイナミクスシミュレーションに注目しました。

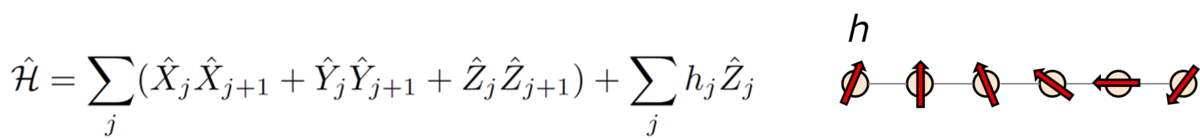
ここで、 ${\small \hat{X}_j, \hat{Y}_j, \hat{Z}_j}$ はそれぞれ ${\small j}$ 番目のスピンに作用するパウリ ${\small X, Y, Z}$ 演算子、 $h_j$ は磁場の強度を表します。

結論として、STARアーキテクチャは100サイトの1次元ハイゼンベルクモデルを発展時間 T=20 程度まで多項式時間でシミュレート可能できることを明らかにしました。このような大規模シミュレーションを正確に実行することは現行のコンピュータでは困難であると予想されますが、量子加速の実現を主張するには今後より詳細な解析が必要になります。

基底状態エネルギーの推定：

物質が最も安定な状態（基底状態）のエネルギーを、量子コンピュータを使って正確に計算することができます。これにより、物質内部の電子系の基底状態エネルギーを計算し、超伝導材料や強相関電子系の特性を予測したり、新しいエネルギー変換材料を設計したりすることに繋がると期待されています。

本研究では特にハバードモデル*8と呼ばれる、高温超伝導体の理論モデルに注目し、STARアーキテクチャ上で必要になるリソース（量子ビット数と計算時間）の見積りを行いました。結果として、STARアーキテクチャは従来のFTQCに比べて必要な量子ビット数を約1/3に削減できると推定されました。また、現行コンピュータによるシミュレーションに比べて、実行時間を1/1000以下に短縮できる可能性も示唆されています。詳細については、過去の記事*9で紹介されていますので、こちらも是非ご参照ください。

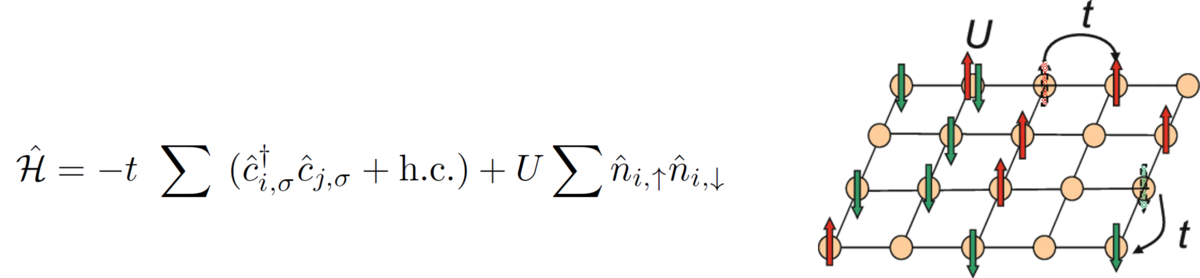
ここで、 $t, U, \hat{c}_{i, \sigma}^{\dagger}, \hat{c}_{i, \sigma}, \hat{n}_{i, \uparrow}, \hat{n}_{i, \downarrow}$ はそれぞれ $i$ 番目の格子の電子のホッピング確率、クーロンエネルギー、電子の生成・消滅演算子、数演算子（スピン上向き・下向き）です。