離散対数問題に対するShorアルゴリズムの実装と量子計算機シミュレータを用いた実験

こんにちは、量子研究所の岸です。富士通研究所ではセキュリティが量子コンピュータにより受ける影響を分析しています。今回は、公開鍵暗号などで使われている離散対数問題に着目して研究成果が得られましたので、その内容を紹介します。この結果は今月の情報セキュリティ研究会でも発表予定です。

論文情報

研究会名：電子情報通信学会情報セキュリティ研究会 (ISEC)
開催日：2023年7月24日(月)～25日(火)
開催場所：札幌市
論文タイトル：離散対数問題に対するShorアルゴリズムの実装と量子計算機シミュレータを用いた実験
著者：岸海斗 (富士通), 山口純平 (富士通), 伊豆哲也 (富士通), 國廣昇 (筑波大学)

背景

公開鍵暗号の一つとして知られる Diffie-Hellman 鍵共有やデジタル署名の一つである DSA 署名では離散対数問題の困難さを利用して安全性を保証しています。離散対数問題にはいくつかの種類がありますが、よく利用される代表的なものとして、素体上の離散対数問題があり、それは次のようなものです：

$p-1$ を $q$ が割り切るような素数 $p,q$ について、 $g^{q} \equiv 1 \mod p$ を満たす自然数 $g$ と $h$ が与えられたとき、 $g^{s}\equiv h\mod p$ を満たす自然数 $0\leq s\lt q$ を求める問題

離散対数問題の具体例として、次の問題を考えます：

$p=11,q=5$ について、 $g=3,h=5$ のとき、 $3^{s} \equiv 5 \mod 11$ となる $s$ は？

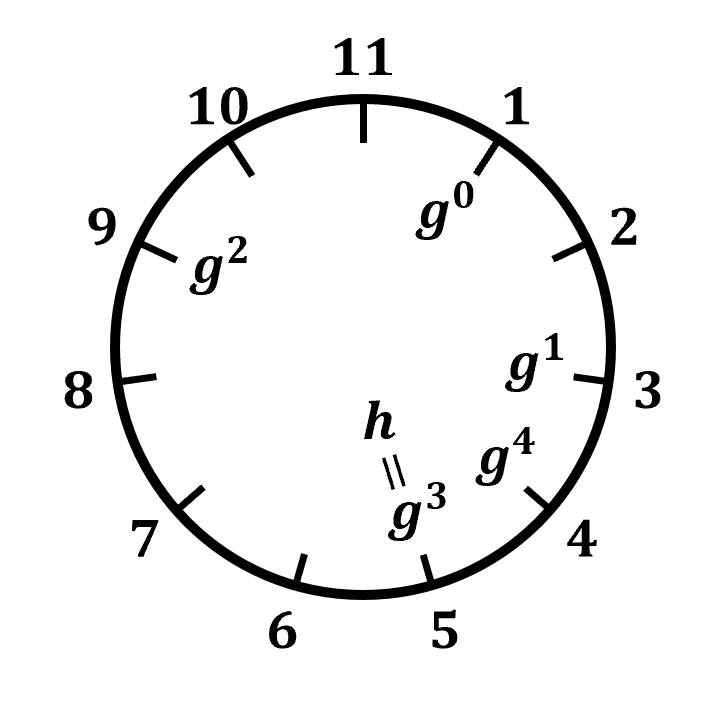
この答えは $s=3$ となります。確かに $3^{3}=27$ を $11$ で割った余りは $5$ となることから確認できます。このことは、以下の時計盤のような図を用いると理解しやすいです。つまり、 $g$ の冪乗を $g^{0}=1,g^{1}=3,g^{2}=9$ と計算していくと、 $g^{3}$ で時計盤を一回りして再び同じ数ではないものの小さな数となります。それがちょうど今回の $h=5$ と一致しています。それから $g^{4}$ でまた一回りし、そして $g^{5}(=g^{q})$ で $g^{0}=1$ に戻ってくることになります。

素因数分解と離散対数問題の大きな違いとして、パラメータの個数が挙げられます。素因数分解では素因数分解する対象である合成数の大きさのみが問題の難しさを決めていますが、離散対数問題では $p$ と $q$ の 2 つが問題の難しさに関わっています。ゆえに、離散対数問題を暗号に用いる際のパラメータの決め方も複数存在し、特に次の 2 通りが使われています：

パターン1: $p$ を安全素数とする
$p$ と $q$ 双方ともに最も大きくするため、 $p$ を安全素数、つまり $p=2q+1$ を満たすように設定するものです。現実によく使われてるケースでは $p$ を 2048 ビット、 $q$ を 2047 ビットとしています。
パターン2: $p, q$ 依存の計算量を一致させる
離散対数問題を解くアルゴリズムとして、数体篩法は $p$ の大きさに、平方根法は $q$ の大きさに依存して解くのにかかる時間が決まります。このパターンはその 2 つの時間が一致するように $p$ と $q$ を設定するものです。現実によく使われてるケースでは $p$ を 2048 ビット、 $q$ を 256 ビットとしています。

この 2 つのパターンを比べると、パターン 2 ではパターン 1 と比べて $q$ を小さくすることができます。これにより、 $p$ の大きさはパターン 1 と変わらないため解くのにかかる時間は変わらないにもかかわらず、防御側にとっては扱いやすい大きさの値とすることができ、 DSA 署名などで特によく使われています。現在求められている離散対数問題の最大の大きさは $p$ が 795 ビットであり*1、ゆえに、上記 2 つのパターンにおけるビットの大きさの設定で安全であるとされています。

一方、素因数分解と同様に Shor が開発した量子アルゴリズム（Shor アルゴリズム）により、従来よりもごく短時間で離散対数問題を解くことができると知られています*2。ただし、やはり素因数分解と同様に、 Shor アルゴリズムはエラー耐性のある数千オーダーの量子ビットを必要とするため、これが実現するまでは相当な時間が必要と考えられています。それでも、その実現にはどれだけの量子ビット数が必要で、どのような性質を持つかを調べておくことは求められています。

離散対数問題を解く Shor アルゴリズム

離散対数問題を解く Shor アルゴリズムは量子計算パートと古典計算パートに分けることができます。

量子計算パート

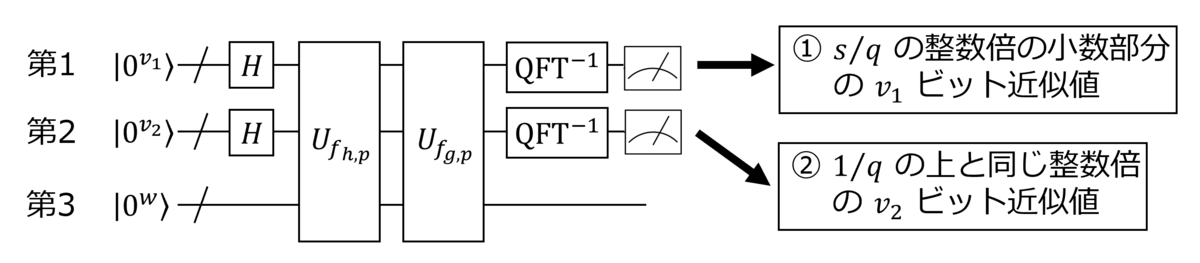
$v_1, v_2, w$ ビットの量子状態 $|0^{v_1}\rangle, |0^{v_2}\rangle, |0^{w}\rangle$ を用意します
第 1, 2 量子ビット列に Hadamard 演算 $H$ を作用させます
第 1, 2 量子ビット列をそれぞれ入力として第 3 量子ビット列に冪剰余計算を実行します。つまり、 $f_{a,p}(x)=a^{x}\mod p$ を実現するユニタリ演算として $U_{f_{g,p}}U_{f_{h,p}}$ を作用させ $h^{x_{1}}g^{x_{2}}\mod p$ を得ます
第 1, 2 量子ビット列にそれぞれ逆フーリエ変換 $\mathrm{QFT}^{-1}$ を作用させます
第 1, 2 量子ビット列を測定します（得られた値をそれぞれ①, ②とします）

このうち、 3. の冪剰余計算が最も時間のかかる部分であり、そのユニタリ演算を実現する方法としては主に 3 つのものが知られています。詳しくは今回の発表の共著者である山口が書いた論文*3をご覧ください。今回の研究ではなるべく大きな $p, q$ のペアで実験するため、量子ビット数を最も少なく抑えられる手法を用いています。

最後の 5. で得られた 2 つの値①, ②を用いて、次の古典計算パートにて $s$ を求めます。

古典計算パート

$q$ を①, ②に掛けたうえで四捨五入します。こうして得られた値を①', ②'とします
$s=$ ①'/②' $\mod q$ と得ることができます

なお、このときの必要な精度を計算することにより、 $v_{1}=v_{2}=\lfloor \log_2 q\rfloor+1$ であるとわかります。このことは本研究において明確にしました。（一方、 $w=\lceil \log_2 p \rceil$ です）

本研究の主な成果

われわれは本研究にて、

32 量子ビットまでで実現可能な $p,q$ のすべての組合せ 1860 通りを解く Shor アルゴリズムをシミュレートし、そこから $p$ が 2048 ビットのときに必要となるリソースを推定しました
推定結果から、古典計算ではパターン 1 とパターン 2 は同じ時間で解かれるにもかかわらず、量子計算ではパターン 2 の方が簡単に解けることを明らかにしました

前者については、スーパーコンピュータ「富岳」に使われる CPU「A64FX」を搭載した「FUJITSU Supercomputer PRIMEHPC FX700」を利用して、量子シミュレータ mpiQulacs*4 による実験を行いました。その結果、解 $s$ はすべて正しく求まり、そのうえで以下のような結果が得られました：

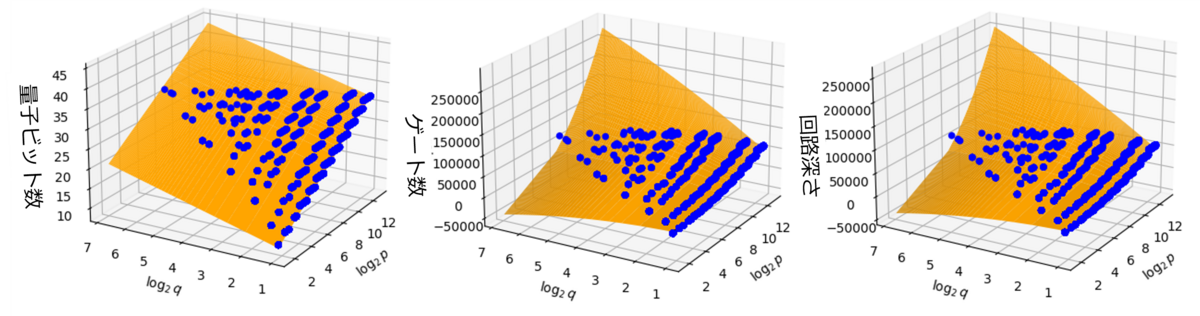
1860 個の青点は、それぞれの $p,q$ の組合せにおける生成された量子回路で必要とされたリソースの値を示しています。そして、オレンジ面は、それらの結果をもとにフィッティングした結果を示しています。

この 1860 通りの実験結果から得られた量子ビット数・ゲート数・回路深さの情報をもとに、われわれはパターン 1 とパターン 2 それぞれで $p$ が 2048 ビットのときの予測を行いました。その結果、量子ビット数を最も抑えられる手法を用いる場合には、以下のようなリソースが必要になると得られました：

( $p$ のビット数, $q$ のビット数)	パターン 1 (2048 ビット, 2047 ビット)	パターン 2 (2048 ビット, 256 ビット)
量子ビット数	$8194$	$4612$
ゲート数	$2.01\times 10^{14}$	$2.52\times 10^{13}$
回路深さ	$1.98\times 10^{14}$	$2.47\times 10^{13}$

ここから後者で述べた、パターン 1 と 2 における必要なリソースの違いが見えてきます。つまり、量子計算では、パターン 2 はパターン 1 のおよそ半分の量子ビット数、約 1/10 のゲート数・回路深さしか必要としないとわかりました。こうしてわれわれは、パターン 1 とパターン 2 は従来の古典計算では解くのに必要な時間に差が存在しない一方、量子計算では差が存在すると明らかにすることができました。

これより詳しい内容は理論的な側面も踏まえて先述した研究会にて発表するので、よろしくお願いいたします。

参考文献

離散対数問題と並んで重要な素因数分解の研究については、

をご覧ください。

*1:F. Boudot et al., “Comparing the Difficulty of Factorization and Discrete Logarithm: A 240-Digit Experiment”, CRYPTO 2020, LNCS 12171, pp. 62-91, Aug 20.

*2:P. Shor, "Algorithms for quantum computation: discrete logarithms and factoring", FOCS 1994, pp.124-134, IEEE, November 1994.

*3:J. Yamaguchi et al, “Estimation of Shor’s Circuit for 2048-bit Integers based on Quantum Simulator”, Cryptology ePrint Archive, Paper 2023/092, January 2023.

*4:S. Imamura et al., “mpiQulacs: A Distributed Quantum Computer Simulator for A64FX-based Cluster Systems”, arXiv: 2203.16044, 2022.