AISTATS2021に採択された論文"The Spectrum of Fisher Information of Deep Networks Achieving Dynamical Isometry"について紹介します. AISTの唐木田亮さんとの共著です.
この記事の筆者：人工知能研究所 自律学習PJ 早瀬友裕（博士 数理科学）
コントロール可能な深層学習を目指して
深層回路（DNN）は画像認識のコンテスト(ILSVRC2012)で圧倒的な性能を示してから, 機械学習の有力な手法として注目されてきました. それからしばらく, DNNの層数はどんどん増えていきました (Fig. 1). 深くすればするほど性能が良くなるのでしょうか？そもそも深層回路はどんなに深くても（＝層数が多くても）学習できるのでしょうか？実験的な検証は行われていますが, これらの問の全容はまだ明らかになっていません.
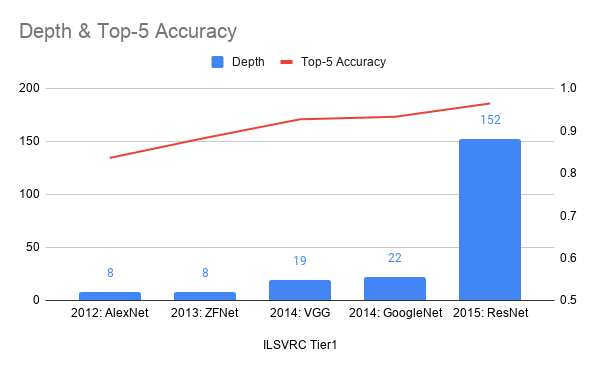
今回の研究は, 深層回路はどんなに深いネットワークでも学習できるのか？と関連する話です. 近年, 様々な研究によって, 深層回路の理論・数理が探求されてきました. その重要なテーマとして以下の 三つがあります.
- 表現能力: その深層回路はあらゆる関数を近似できるか？
- 学習可能性: 勾配降下法で最適化できるか？高速に最適化するには？学習率の良い設定方法は？
- 汎化性能: 訓練データに過学習しないか？（過学習とは, 人間でいえば計算ドリルの答えを丸暗記してテストで答えられないようなものです. ）
今回の研究は学習可能性に分類できます.
Edge of ChaosとDynamical Isometryと勾配消失発散問題
層数が増えるとどのような問題があるのでしょうか？DNNは大抵確率的勾配降下法(SGD)で学習されます. DNNの勾配は, 微分の連鎖律から各層の勾配行列の積になります. 従って, パラメータの初期値や活性化関数のナイーブな設定の下では, 層数が増えるごとに指数的に勾配が消失・発散し学習できなくなってしまうのです. これが古くから知られているDNNの勾配消失発散問題です.
勾配消失発散を防ぐため, 以下の性質が調べられてきました (Saxe et. al., 2014, Pennington et al., 2018, Xial et al., 2018, Sokol and Park 2020)：
- Edge of Chaos: 層を跨いで勾配の二乗平均が保たれる.
- Dynamical Isometry: DNNの入力に関するJacobianの特異値が層数増加に対し定数オーダー.
Dynamical Isometry はEdge of Chaosよりも強い性質です. 特に, Xiao et. al., 2018ではDynamical Isometryを満たすようにDNNを調整することで, 10000層のCNN (Convolutional Neural Network, DNNの一種)を実際に学習してみせました. 特にBatchNormやResidual Connectionを使っていません.
この結果により, 層は深くなっても学習できるということが実験で示されました. また, Pennington et al., 2018では, MLP(Multilayer Perceptron, DNNの中で最も基礎的なもの)がDynamical Isometryを満たすためには, 直行初期化と活性化関数の正規化を用いればよいことが理論的に分かりました. ちなみに, よくあるガウス初期化とReLU活性化関数の組み合わせではDynamical Isometryは達成できないことも理論的にわかります.
DNNの学習ダイナミクスとFisher情報行列
では, もう一歩踏み込んで, Dynamical Isometryの条件下で, 学習率や学習アルゴリズムをどのように調整すればよいでしょうか？ もっと一般に, Dynamical Isometry下でDNNの学習ダイナミクスはどのようになっているでしょう？この問いに答えるため, 今回はDNNのFisher情報行列を調べます. なぜならば, Fisher情報行列はロス曲面の曲がり具合を決めるからです. Fisher情報行列は数理統計学や情報幾何学において昔から知られていますが, 深層学習でも重要です (Karakida et al., 2019).
注) Dynamical Isometryより後に考案されたNeural Tangent Kernel (Jacot et al, 2018)はFisher情報行列のある種双対の存在です. こちらもDNNの学習ダイナミクスを理解するのに重要ですが, Dynamical Isometryの設定と多少異なる部分（最終層の幅など）があるので注意が必要です.
論文の貢献
今回の研究では自由確率論という数学を用いて, いくつかのことが分かりました. 最も重要なものは以下の結果です.
- MLPがDynamical Isometryを満たすとき, サンプルごとのFisher情報行列の（ゼロ以外の）固有値は, 最大固有値に集中する. 最大固有値は層数に比例する (Hayase and Karakida 2021, Theorem 4.3).
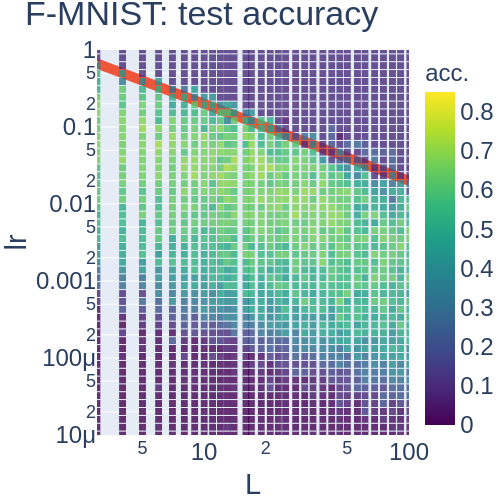
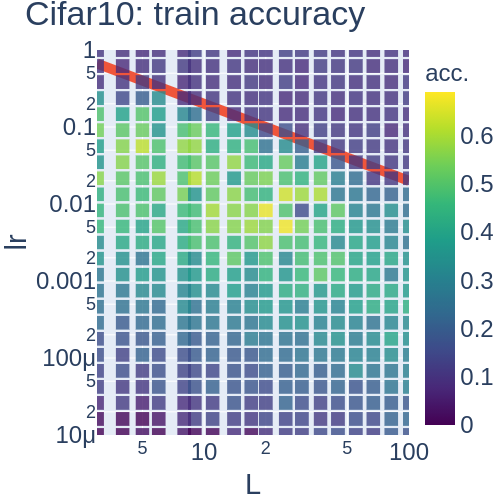
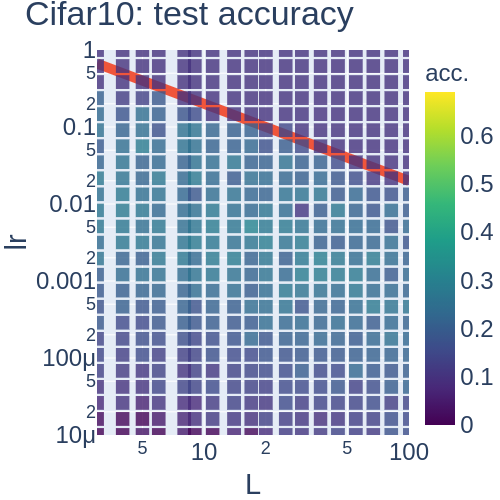
ここで, 最大固有値が層数に応じて増えるのは想像に難くありませんが, 最大固有値に集中することは非自明です. このことから, 学習率は層数に反比例して設定すればよいということが推論できます. また, 実験の結果とピッタリ合っています (Fig. 2). 強調すべきは, Dynamical Isometry下ではJacobianの特異値は層数に依存しないのに, Fisher情報行列は層数に依存するという点です.
議論
副次的結果として, 層数が浅い場合に, Fisher情報行列（サンプル毎）の特異値分布を(幅無限の極限で)陽に書くことができました (Figure 3).
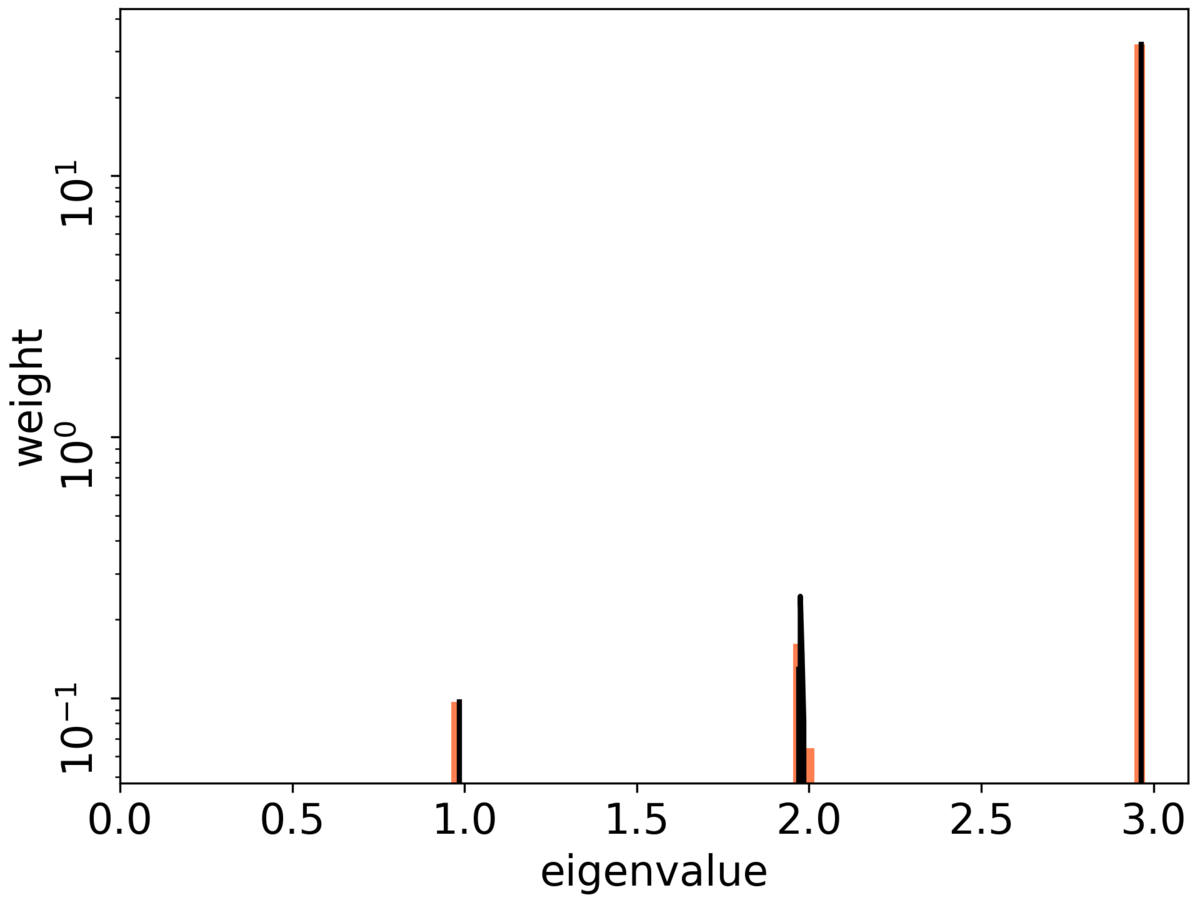
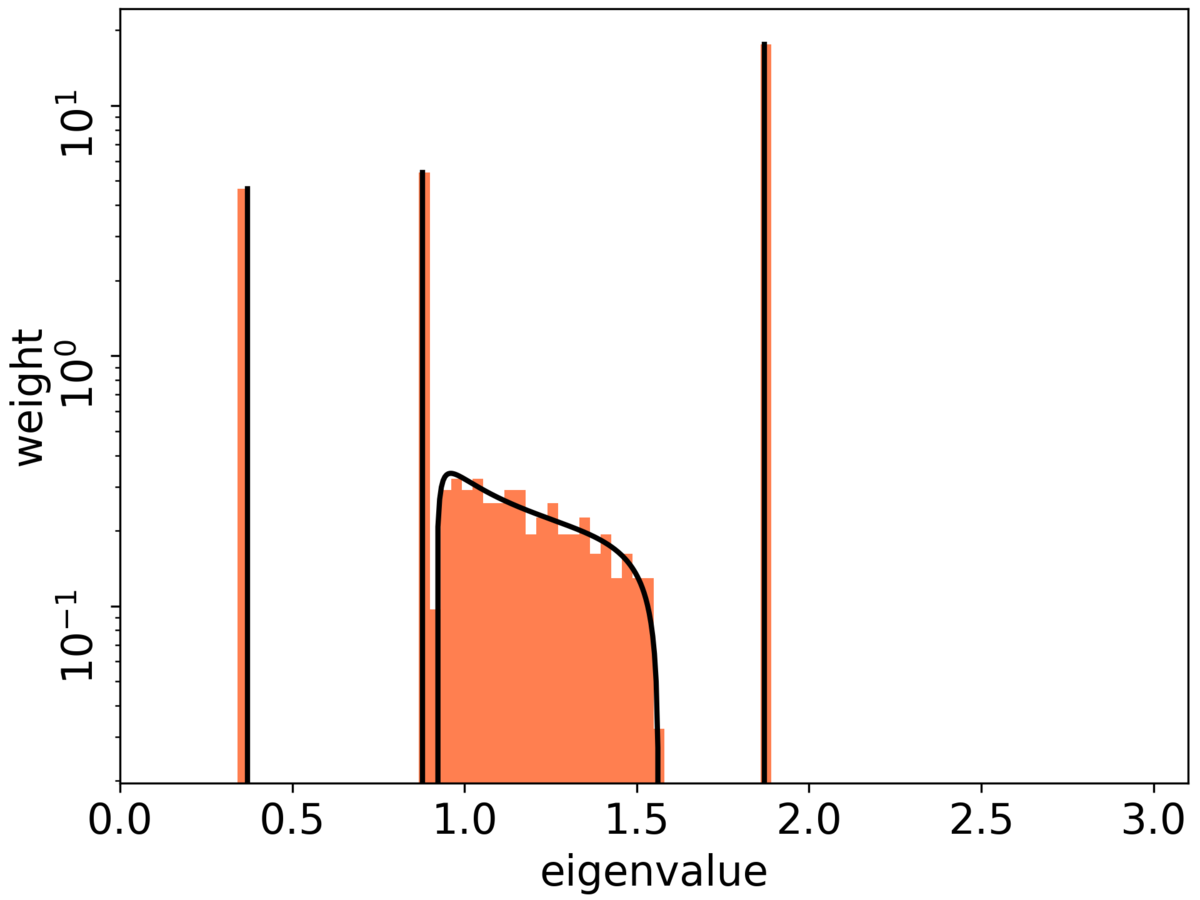
おわりに
DNNの学習ダイナミクスの解析において, しばしばランダムネットワークの設定が使われます. この設定で学習初期の様子が分かるという点も大事ですが, それだけではありません. 実は適切な条件(NTK-regime (Jacot et al. 2018) ) のもとで学習ダイナミクスが初期化時点で分かることが知られています. また, パラメーターひとつひとつではなくてパラメーターの統計性に注目しているとも言えます. まとめると, ある程度DNNの性質を定性的に大雑把に知りたいとき, 特に幅や深さが大きくなっていく漸近的な挙動を知りたい場合, ランダムネットワークを調べることが有効です.
謝辞
この研究は主にJST ACT-X「数理・情報のフロンティア」領域「自由確率論による深層学習の研究」と「大自由度ニューラルネットワークの学習に潜む幾何学的構造の解析と信頼性評価への展開」の一環として援助を受け行われました.
参考文献
Ryo Karakida, Shotaro Akaho, and Shun-ichi Amari. "Universal statistics of Fisher information in deep neural networks: Mean field approach." In Proceedings of International Conference on Artificial Intelligence and Statistics (AISTATS), 1032-1041, 2019.
Arthur Jacot, Franck Gabriel, and Clément Hongler. "Neural tangent kernel: Convergence and generalization in neural networks." In Advances in neural information processing systems (NeurIPS), pages 8571–8580, 2018.
Jeffrey Pennington, Samuel Schoenholz, and Surya Ganguli. "The emergence of spectral universality in deep networks." In Proceedings of International Conference on Artificial Intelligence and Statistics (AISTATS), pages 1924–1932, 2018.
Andrew M Saxe, James L McClelland, and Surya Ganguli. "Exact solutions to the nonlinear dynamics of learning in deep linear neural networks." ICLR 2014, arXiv:1312.6120, 2014.
Lechao Xiao, Yasaman Bahri, Jascha Sohl-Dickstein, Samuel S Schoenholz, and Jeffrey Pennington. "Dynamical isometry and a mean field theory of CNNs: How to train 10,000-layer vanilla convolutional neural networks." In Proceedings of International Conference on Machine Learning (ICML), pages 5393–5402, 2018.
